Wie gebe ich einen Funktionsterm in einen Taschenrechner ein? (Newtonverfahren)

Question

Aufgabe:

f(x)=x3+32x2+99
abgeleitet: f(x)= 3x2+64x

f(-32)= (-32)3+32*(-32)2+99= 99

f'(-32)= 3*(-32)2+64*(-32)=1024

x1= -32-(99/1024) =32.09667969

x2= -32.09667969-(-32.09667969/-32.09667969) = -33.09667969 (falsch)

Habe bis jetzt schon herausgefunden, dass man f(-32.09667969)/f'(-32.09667969) in den Taschenrechner eingeben muss.... wie?

Comments

Da musst du schon den Typ Taschenrechner nennen. Außerdem bitte ich dich, Exponenten auch wirklich nach oben zu schreiben.

---

Ups, wurde falsch kopiert.

Habe den Casio-FX 99

---

Vgl. https://www.mathelounge.de/506016/matheartikel-das-newtonverfahren-frage 

Bitte Duplikate vermeiden! 

---

Meiner Auffassung nach, sind das zwei verschiedene Fragen

---

Ohne den Link kann man die Exponenten nur erraten und zudem soll ja Gorgar morgen nicht denken, dass du immer noch auf eine Antwort wartest! 

---

Hi,

habe geschrieben:

"Schade... Naja mal schauen vielleicht komm ich ja selbst drauf..."

------->

Ich antworte im ja erst, wenn ich es verstanden habe, oder nicht?

Akutell könnte er mir ja noch Hilfe leisten...

LG

Answer 1

Hi,

du musst die Steigung und den Funktionswert an der Stelle \(x_1\) berechnen und einsetzen: \(x_2=x_1-\frac{f(x_1)}{f'(x_1)}\)

Comments

Geht das vielleicht in Zahlen anhand von einem Beispiel? (sonst verstehe ich nichts)

LG

---

Du hast folgendes gerechnet: \(x_2=x_1-\frac{x_1}{x_1}\)

Du sollst aber \(x_2=x_1-\frac{f(x_1)}{f'(x_1)}\) berechnen.

\(f(x_1)=-0.599111818776679440814209\)

und 

\(f'(x_1)= 1036.4030412073754883\)

Somit erhältst du: \(x_2=-32.09667969 +\frac{-0.599111818776679440814209}{1036.4030412073754883} \approx -32.09725776\)

Es ist wichtig, dass du auch die Formel \(x_{i+1}=x_i+\frac{f(x_i)}{f'(x_i)}\) verstehst. Versuche das mal. In unserem Fall war \(i=1\).

---

Wie sind Sie denn auf die beiden Zahlen gekommen

f(x1)= 0.599...

f'(x1)= 1036.403.....

---

Du kannst mich ruhig duzen :)

Ich habe die \(x_1\) in \(f(x)\) bzw. \(f'(x)\) eingesetzt und mit dem Taschenrechner ausgerechnet.

---

Bin nicht Experte auf dem Gebiet... Dieses Thema erfordert sehr viel verständnis das ich nicht besitze (falls manche Fragen dümmlich erscheinen)

Und wie gibt man das exakt ein? habe ja kein f auf meinem Taschenrechner... (denke ich)

---

Macht nichts, die Seite ist ja dazu da um Fragen zu stellen :)

Ein \(f\) hast du in der Tat nicht, aber du kennst deine Funktion, die \(f\) heißt. Du hast ja auch \(f(-32)\) und \(f'(-32)\) berechnet. Genauso berechnest du \(f(x_1)\) und \(f'(x_1)\).

Da du bei den Grundlagen auch noch Probleme hast, empfehle ich dir beispielsweise mal dieses Video anzuschauen:

---

"Ich habe die x1 in f(x) bzw. f'(x) eingesetzt und mit dem Taschenrechner ausgerechnet"

Wie macht man das? Habe einen Casio FX-99

---

Du hast doch auch \(f(-32)\) berechnest. Genauso berechnest du \(f(x_1)=f(-32,09667969)\).

Statt \(x\) tippst du in \(f(x)=x^3+32x^2+99\) die Zahl \(-32,09667969\) in deinen Taschenrechner ein.

---

Danke,

Jetzt habe ich es verstanden!

MfG

---

Beispiel:

f(x)=x^3+32x^2+99
abgeleitet: f(x)= 3x^2+64x

f(-32)= (-32)^3+32*(-32)^2+99= 99

f'(-32)= 3*(-32)^2+64*(-32)=1024

x1= -32-(99/1024) =32.09667969

f(x1)= (-32.09667969)^3+32*(-32.09667969)^2+99 = -0.5991118187

f(x2)= 3*(-32.09667969)^2+64*(-32.09667969)≈ 1036.403041

x2= -32.09667969-(-0.5991118187/1036.403041)= -32.09610162

---

Bitteschön. 

Fast richtig, ganz unten bei \(x_2\) hast du zwei mal in Minus, wodurch du ein Plus bekommst.

Es musst \(x_2=-32.09667969+\frac{-0.5991118187}{1036.403041}\) sein.

---

Wie wäre es eigentlich wenn

f(x)= x^5+32x^2+99

abgeleitet: f(x)= 5x^2+64x

Ist es dann:

f(-3.4)= (-3.4)^5+32*(-3.4)^2+99= 14.56576

f'(-3.4)= 5*(-3.4)^5+64*(-3.4)=-2489.3712

-3.4-f/f'= -3.405....

---

Ich habe jetzt nicht extra nachgerecht, aber habe mir den Graphen mal angeschaut. -3,4 ist eine gute Wahl und deine Vorgehensweise ist auch vollkommen korrekt :)

---

Ich habe mir gerade die Frage gestellt, ob man, um einen ungefhähren Wert zu erlangen, einen Plotter benutzen muss. Oder ist es möglich einen Nährwert der Funktion zu entnehmen oder gar auszurechnen?

---

Du kannst zufällige Werte einsetzen und schauen wann was negatives als Ergebnis kommt und wann was positives. Sagen wir mal \(x_10\). Da die Funktion stetig ist, weißt du nun, dass sie eine Nullstelle im Intervall \( (x_1,x_2 \) hat. Nun kannst du z. B. schauen, ob \(f(x_2/2)>0 \) oder (f(x_2/2)<0 \). Ist ersteres der Fall, so gibt es eine Nullstelle im Intervall \(x_1,x_2/2 \). Anderenfalls gibt es eine Nullstelle im Intervall \( x_2/2,x_2 \). Und so weiter. Allgemein kannst du auch noch Teiler des Werts des y-Achsenabschnitts, hier also 99, austesten. Jede ganzzahlige Nullstelle ist ein Teiler des Werts des y-Achsenabschnitts.

Answer 2

Hallo Anton! :-)

Es folgen zwei Beispiele, wie du die Nullstellen einer Funktion mit deinem Taschenrechner berechnen kannst.
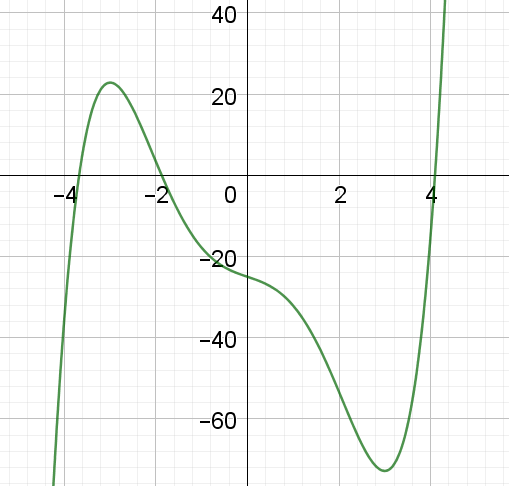
Die Funktion ist
f(x) = 0,25x^5 - 3,6x^3 - 3,8x - 25 mit ihrer Ableitung
f'(x) =  1,25 x^4 - 10,8 x^2 - 3,8

1) Direktes Lösungsverfahren - Die Lösung wird nach der Eingabe der Funktionsgleichung und des Startwertes ohne Zwischenergebnisse angezeigt. Eingabe der Funktionsgleichung y = 0,25x^5 - 3,6x^3 - 3,8x - 25

Startwert x = -4
Nullstelle x ≈ -3.675799231

Startwert x = -2
Nullstelle x ≈ -1.872647415

Startwert x = 4
Nullstelle: x ≈ 4.094346966

2) Eingabe der Formel - Die Näherungen(Zwischenergebnisse) werden angezeigt.
Eingabe der Formel: x = x - (0,25x^5 - 3,6x^3 - 3,8x - 25) / (1,25 x^4 - 10,8 x^2 - 3,8)

Startwert: x = -4
Abgelesene Zwischenergebnisse

x1 = -897/239 ≈ -3,753138075
x2 ≈ -3,681593773
x3 ≈ -3,675835072
x3 ≈ -3,675799233
x4 ≈ -3,675799231

Ab x4 ≈ -3,675799231 ändern sich die Werte nicht mehr, die Genauigkeit des Taschenrechners hat seine Grenze erreicht.

Grüße

Comments

Vielen Dank,

Der Aufwand deiner Antworten ist atemberaubend.

Hochachtungsvoll,

Anton

---

Anton, könntest du vielleicht noch kurz erwähnen, in welchem Schuljahr du bist?