Ich habe das so gerechnet. Muss man nicht die 0,5… mitnehmen? Ich verstehe das iwie nicht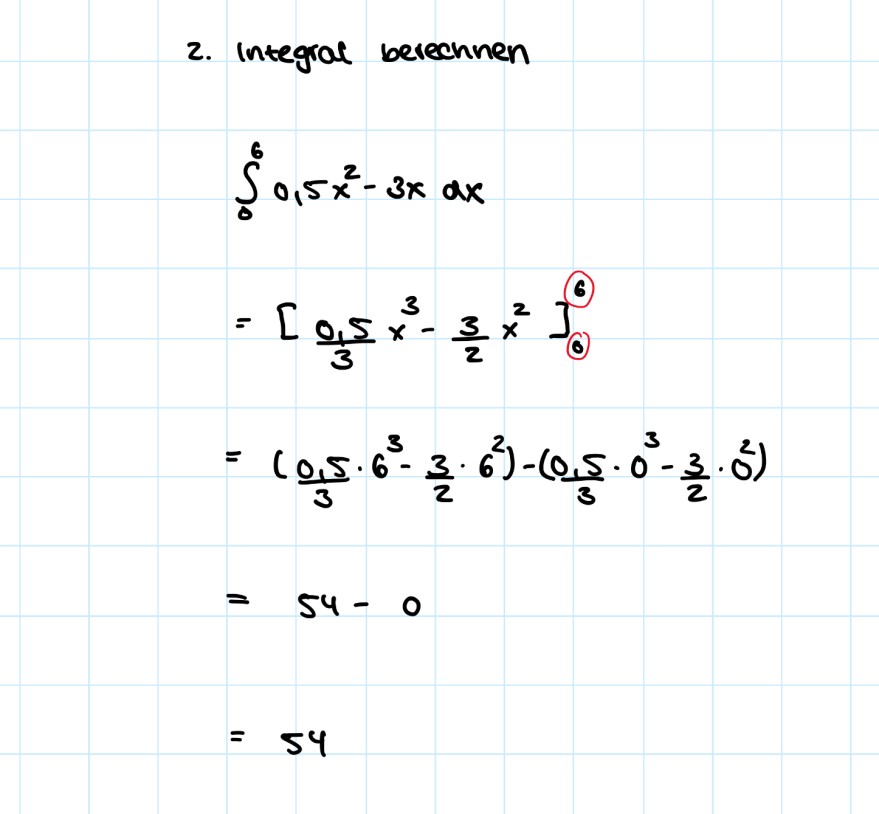
Text erkannt:
2. integral berechnen
\( \begin{array}{l} \int \limits_{0}^{6} 0,5 x^{2}-3 x d x \\ =\left[\frac{0,5}{3} x^{3}-\frac{3}{2} x^{2}\right]_{0}^{6} \\ =\left(\frac{0,5}{3} \cdot 6^{3}-\frac{3}{2} \cdot 6^{2}\right)-\left(0,5 \cdot 0^{3}-\frac{3}{2} \cdot 0^{2}\right) \\ =54-0 \\ =54 \end{array} \)