Das Volumen einer Kugelschicht berechnen

Question

Meine Aufgabe lautet wie folgt : 

Gegeben ist eine Kugel mt dem radius r= 100cm. Von der Kugel sollen oben und unten je ein Kugelabschnitt mit gleicher höhe abgeschnitten werden. Den verbleibenden Kugelrest nennt man kugelschicht. 

a) Berechne das volumen der kugeschicht wenn beide Kugelabschnitte die höhe h= 10cm haben.

b) Zeichne den graphen für das volumen der kugelschicht in abhängkeit von der höhe h der kugelabschnitte.Notiere  die zugehörige formel

c) Für welche höhe h der kugelabschnitte ist das volumen der kugelschicht genau halb so groß wie das volumen der kugel

Comments

https://de.wikipedia.org/wiki/Rotationskörper#Rotation_um_die_x-Achs… gibt dir mal die möglichen Formeln. Mache eine geeignete Skizze und wähle Koordinatenursprung geeignet. Mantellinie und Integrationsgrenzen ergeben sich dann automatisch. (Symmetrie kann man auch ausnützen)

---

Ich habe für die aufgabe a als ergbeniss V= 4158421,48 ...... wäre echt erleichtert wenn jemand das gleiche herausgefunden hat und wenn nicht ob er mir dann sein ergebnis erklären könnte   ☺☺

---

Nein, das stimmt nicht, ich habe 4128052,747ccm heraus, ein Kugelsegment hat den Inhalt von 30368,729 ccm und die gesamte Kugel hat einen Inhalt von 4188790,205 ccm.

---

V= 4158421,48

@the biggest loser
Du hast nur ein Mal das Volumen des Kugelabschnitts vom Volumen der Kugel abgezogen.

Answer 1

r = 50 cm
f ( x ) = √ ( 50² - x² )
A ( x ) = [ f ( x ) ] ² * π = ( 50 ² - x² ) * π
Stammfunktion
∫ A ( x ) dx = ∫  ( 50 ² - x² ) * π dx
π * ∫  50 ² - x²  dx
π * ( 50 ² * x - x³ / 3 )

halbseitige Berechnung
Kugel
[ S ( x ) ] zwischen 0 und 50
π * ( 50 ² * 50 - 50³ / 3 )
261799 cm³

Volle Kugel : 261799 * 2 = 523598 cm³

Kugelmitte minus Kugelschnitt
[ S ( x ) ] zwischen 0 und 40
π * ( 50 ² * 40 - 40³ / 3 )
247139

Voller Wert : 247139 * 2 = 494278 cm³

Manchmal verschwinden meine Kommentare.

Hier noch die Skizze#

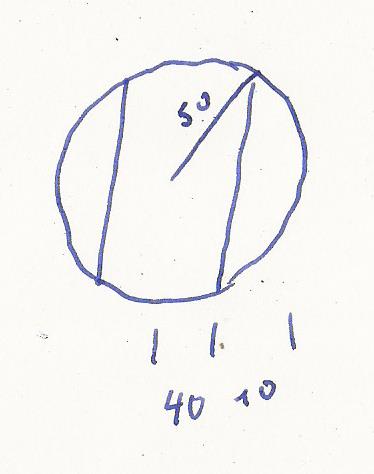Kann jemand einen Fehler entdecken ?

Comments

Ich habe die Formel für das
Kreissegment bei Wikipedia einmal
nachgeschaut.
1 Kreissegment 14660
beide 29322
Volle Kugel minus Kreissegmente
523598 - 29322 = 494276 cm³

---

@georgborn: Ist dein Kommentar eine Frage? Du hast wohl irgendwo einen Rundungsfehler. So genau kann dein Ergebnis nicht sein, wenn die Zwischenresultate nicht genauer sind als das Endresultat. 

---

Hallo Lu, da mein Ergebnis von den anderen
Ergebnissen abgewichen ist habe ich in meinem
Kommentar nochmals nach Formeln berechnet.
Mein Ergebnis hat sich bestätigt.

Alle Berechnungen wurden mit einem
Matheprogramm ermittelt und dann auf
ganze Zahlen gerundet.

---

"Alle Berechnungen wurden mit einem
Matheprogramm ermittelt"

Darum erstaunt mich die Abweichung. 

494278 cm³

494276 cm³

---

Hallo Georg, warum rechnest du mit r=50 cm?

Answer 2

Hallo

V_Kugelschicht = V_Kugel  - 2·V_{Kugelabschnitt}
V_Kugelschicht = 4/3·π·r³ - 2·(1/3·h²·π·(3·r - h))

V_Kugelschicht = 4/3·π·100³ - 2·(1/3·1²·π·(3·100 - 10))

V_Kugelschicht = 4128052,748 cm³  (4128,05 Liter)

https://de.wikipedia.org/wiki/Kugelsegment

Grüße

P.S.

b) h in dm, V in Liter.

 c)

h in Dezimeter

$V_{Kugelschicht} = \frac{1}{2}V_{Kugel}$
$\frac{4}{3}\pi\cdot 10^3 - 2\left(\frac{1}{3}h^2\cdot \pi\left(30-h \right) \right) = \frac{1}{2}V_{Kugel}$
...
Nach einigen Umformungen bekommen wir die kubische Gleichung
$2h^3 - 60h^2 + 2000 = 0$

mit der Lösung
$h = 10 - 20\sin\left(\frac{\pi}{18} \right)$
$h \approx 6,527 \ dm$ (beide Höhen zusammen)