Inverse Matrix Textaufgabe

Question

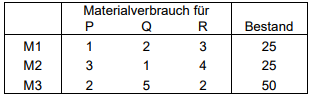
Für die Herstellung der Erzeugnisse P, Q und R sind die Materialien M1, M2 und M3 erforderlich. Die
folgende Tabelle gibt den Materialverbrauch pro Einheit und den verfügbaren Bestand an.

Zu bestimmen ist, wie viele Einheiten der Erzeugnisse mit dem vorhandenen Material hergestellt werden
können.
a) Formulieren Sie die Aufgabenstellung als lineares Gleichungssystem in Matrixschreibweise.
b) Lösen Sie das LGS mit Hilfe der Inversen der Koeffizientenmatrix.

Meine Vorgehensweise  

1 2 3        P       25                    1 2 3 1 0 0                    -0,72 0,36 -0,2        25          1

3 1 4    *  Q  =   25        --->      3 1 4 0 1 0        A^-1 =     0,08 -0,24 -0,2   *  25     =    6

2 5 2       R       50                    2 5 2 0 0 1                     0,52 0,04 -0,2        5 0          4

                                                                                     

                                                                                     3

Das habe ich raus nur soll das Ergebnis der Vektor    8   sein , Die Inverse ist richtig , das habe ich schon kontrolliert . habe ich die Gleichung falsch aufgestellt?                

                                                                                    2

                                                                                       

Answer 1

[1, 2, 3; 3, 1, 4; 2, 5, 2]·[x; y; z] = [25; 25; 50] --> [x; y; z] = [3; 8; 2]

Oder mit der Inversen

[1, 2, 3; 3, 1, 4; 2, 5, 2]^{-1}·[25; 25; 50]

= [-0.72, 0.44, 0.2; 0.08, -0.16, 0.2; 0.52, -0.04, -0.2]·[25; 25; 50] = [3; 8; 2]