Ordnungsrelationen nachweisen

Question

Zeigen Sie, dass die folgenden Relationen auf den jeweiligen Mengen A Ordnungsrelationen sind und prüfen sie, ob sie linear sind. 

a) A= ℘(B) für eine Menge B, R = {(M,N)|M⊆N}.

b) A = (0,∞),R={(x,y)|x/y≤y/x}

Ich komme in die Aufgabe irgendwie nicht rein, weil ich mir die gegebenen Mengen zu abstrakt sind. 

Ich weiß nicht, wie ich damit die Eigenschaften nachprüfen kann. 

Grüße 

Answer 1

a)  

 >  A= ℘(B) für eine Menge B, R = {(M,N)|M⊆N}.

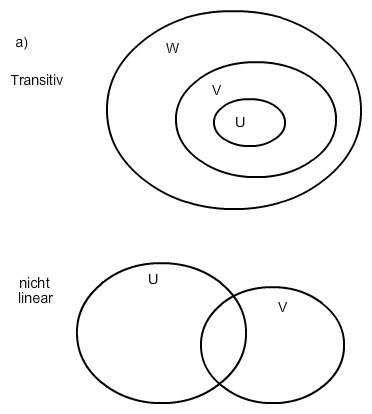
Für eine Ordnungsrelation muss die Transitivität gelten:

(U,V) ∈ R  und  (V,W) ∈ R  → (U,W) ∈ R    für alle U, V, W ∈ ℘(B)

⇔  U⊂V  und   V⊂W  →   U⊂W   für alle U, V, W ∈ ℘(B)  

Das ist offensichtlich wahr. Also ist R eine Ordnungsrelation. 

Linearität:

(U,V) ∈ R  oder (U,V) ∈ R  für alle U, V ∈ ℘(B) 

⇔  U ⊂ V  oder  V ⊂ U  für alle U, V ∈ ℘(B)

Das ist offensichtlich falsch, also ist die Relation nicht linear

b) analog

Gruß Wolfgang

Comments

Hi, danke für deine Antwort.