Flächenberechnung Tangente

Question

Folgende Aufgabe:

Die Normale im Punkt P auf dem Graphen einer Funktion f steht senkrecht zur Tangente in P (siehe Anhang). D.h. es gilt: Wenn m die Steigung der Tangente in P ist, dann ist - 1/m die Steigung der Normalen in P.

a) Berechnen Sie den Inhalt der Fläche, die vom Graphen von f, der Normalen in P und der x-Achse begrenzt wird.

(1) f(x)= -x^2 ; P(1|-1) 

(2) f(x)= x^3 ; P(1|1)

b) Berechnen Sie den Inhalt der Fläche; die vom Graphen der Funktion h mit   h(x)= -x^3 + x   und der Normalen im Wendepunkt von h eingeschlossen wird.

für die Hilfe

Answer 1

(a) 1) f(x)= -x² f'(x)=-2x, f'(1)=-2 Tangente in P:y= - 2x+1 schneidet die x-Achse in(0,5|0)

          Normale in P: y=1/2x-3/2 schneidet die x-Achse in (3|0).

Die Fläche ist ein Dreieck mit der Grundseite 2,5 und der Höhe 1. Flächeninhalt 2,5·1/2=1,25.

Comments

Das ist leider nicht richtig. Es soll nicht die Fläche bestimmt werden die die Tangente mit der normalen und der x achse einschliesst, sondern die Fläche die von graphen der Funktion f, der normalen und der x achse eingeschlossen wird.

---

Du hast recht. Das habe ich nicht aufmerksam gelesen.

Answer 2

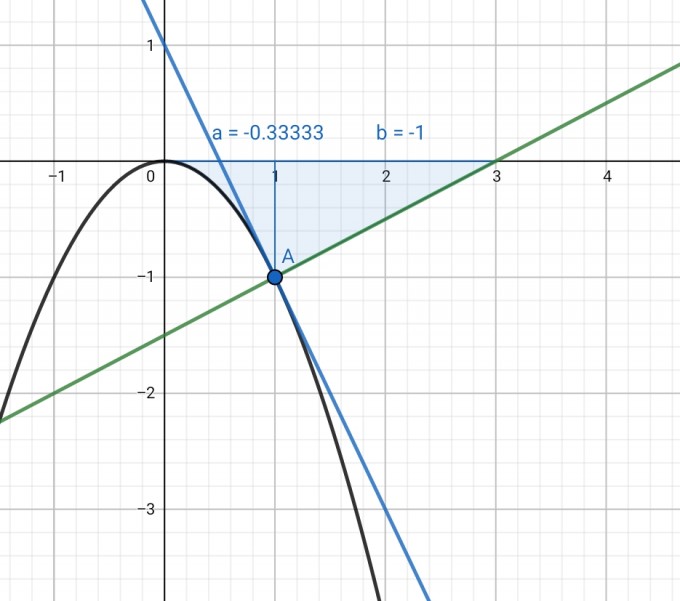
Steigung an der Stelle 1 ist

f'(1)=-2*1=-2

Die Steigung der normalen ist damit m=1/2. Die normale hat die Gleichung

g=1/2*(x-1)-1

   1/2*x-1,5

Die normale schneidet die x-achse bei (3/0)

Damit besteht die gesuchte Fläche aus 2 Teilen. Einem Dreieck unter der normalen zwischen 1<x<3 und der Fläche unter der Kurve zwischen 0<x<1. Hierfür müssen wir integrieren.

F=-1/3*x^3

∫_(0)^1-x^{2} dx=[-1/3*x^3]_(0)^1=-1/3

Damit ist die Fläche unter Kurve also 1/3.

Das Dreieck hat die grundseite 2 und die Höhe 1. Damit ist seine Fläche 2*1/2=1.

Also ist die Gesamtfläche 1+1/3=4/3.

Comments

Hi koffi123, ein Tipp: Du kannst Desmos Links direkt hier posten und sie werden eingebettet.

Siehe zum Beispiel hier: https://www.mathelounge.de/514085/tipp-eingeschlossene-flache-von-graphen-plotten-mit-desmos

---

Hallo mathelounge,

erkennst du die relevanten Zahlenwerte (der Teilintegrale (inkliusive Vorzeichen!)) in koffis Bild? Die fehlen in deinem Link / benötigen dort Zusatzaufwand. 

Answer 3

∫(- x^2, x, 0, 1) + ∫(1/2·(x - 1) - 1, x, 1, 3) = - 4/3

Die Fläche die von der Graphen, der Normalen und der x-Achse gebildet wird beträgt also 4/3 FE.

Das sieht auch graphisch etwa wie folgt aus.