Wie groß ist die Anzahl der zu 9 teilerfremden natürlichen Zahlen < 9? (invertierbare Elemente von Z_9 bestimmen)

Question

Moin!

Es geht um folgende Aufgabe:

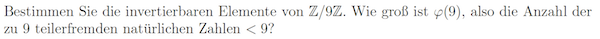
Frage 1:

Die Schreibweise Z_9 kenne ich (alle Elemente der Restklasse 9 aus der Menge der Ganzen Zahlen), 

aber was ist mit Z_9Z gemeint? 

Frage 2:

Ich muss die Frage hier erst einmal auseinander nehmen...

"[...] die invertierbaren Elemente von Z_9"... heißt:

Ich soll für jedes [n]_9 ein invertierbares Element finden, so dass [n]_9 ⊗ [n]_9 = [1]_9 ergibt, korrekt?

Als nächstes... 

"wie groß ist die Anzahl der zu 9 teilerfremden natürlichen Zahlen < 9", bedeutet...

... alle Zahlen von 1 - 8, wovon 3 ein Teiler von der 9 ist. 

Die Antwort wäre also: 

$$\varphi(9) = {2, 4, 5, 6, 7, 8}$$ 

⁉️

Answer 1

1) \(\mathbb{Z}_9\equiv\mathbb{Z}/9\mathbb{Z}\)

2) Es sind tatsaechlich die \(x\in\mathbb{Z}_9\) gesucht, für die ein \(\hat{x}\in\mathbb{Z}_9\) existiert, sodass \(x\hat{x}=1\) ist. Welche das sind, kannst Du aus einer Multiplikationstafel für \(\mathbb{Z}_9\) ablesen.

3) \(\varphi(9)\) ist eine Zahl, keine Liste von Zahlen. Sie stimmt mit der Anzahl der in 2) gefundenen invertierbaren Elemente ueberein. Warum?

Comments

Frage vorweg: wie schreibst du die LaTex-Zeichen (x € Z_9) inline? 

Sobald ich latex-zeichen mit "$$...$$" einfüge, gibt es nen Zeilenumbruch. 

2) 

Alle x' € Z_9 für die xx' = 1 gilt, sind all jene Felder wo eine 1 steht oder? Das wären in diesem Fall 6 Felder...? Weil an 6 Stellen die 1 auftaucht?

Die 9 ist also zu 6 Zahlen aus den Zahlen von 1 - 8 teilerfremd? 

---

1) LaTeX inline geht wie ueblich mit \(\text{\\(}\) am Anfang und \(\text{\\)}\) am Ende der Formel.

2) Jo. In jeder Zeile, in der man eine Eins findet, hat das Element, mit dem die Zeile beschriftet ist, ein Inverses. Und zwar ist es das, mit dem die Spalte, in der die Eins steht, beschriftet ist.

\(a, b\) teilerfremd bedeutet \(\operatorname{ggT}(a,b)=1\). Fuer \(b=9\) findet man \(a=1,\,2,\,4,\,5,\,7,\,8\). Das sind die mit den Inversen von vorher. Macht \(\varphi(9)=6\).

---

Den folgenden Ausdruck:

\( \mathbb{Z_9} \equiv \mathbb{Z}/ 9 \mathbb{Z}\)

... übersetze ich mir zu:

linke Seite: ganze Zahl Modulo 9 ist equivalent zu
rechte Seite: ganze Zahl geteilt durch Modulo 9 mal eine ganze Zahl

mein Verständnis der rechten Seite macht wahrscheinlich keinen Sinn.

Wie muss ich diesen Ausdruck verstehen?