Hallo Frido,
Eine Höhe steht senkrecht auf der dem Eckpunkt gegenüberliegenden Seite. Willst Du z.B. die Gerade \(g_{hc}\), auf der \(h_C\) liegt, bestimmen, so schaue Dir zunächst den Vektor \(\vec{AB}\) an:
$$\vec{AB}= \begin{pmatrix} 7\\ -4\end{pmatrix} - \begin{pmatrix}-5 \\ -1\end{pmatrix} = \begin{pmatrix} 12\\ -3\end{pmatrix}$$ Dieser steht senkrecht auf der Höhe. Man kann ihn also sofort als Normalenvektor für die gesuchte Geradengleichung verwenden (Normalenform). \(C= \begin{pmatrix} 1 & 2\end{pmatrix}^T\) liegt auf dieser Geraden, so lässt sich das \(d\) in \(\vec{n} \vec{x}=d\) berechnen. Vorher teile ich den Normalenvektor noch durch 3, da die Länge keine Rolle spielt \(\vec{n} = \frac13 \begin{pmatrix} 12 & -3 \end{pmatrix} = \begin{pmatrix} 4 & -1 \end{pmatrix}\).
$$g_{hc}: \space \begin{pmatrix} 4\\ -1\end{pmatrix} \vec{x} = \begin{pmatrix} 4\\ -1\end{pmatrix} \cdot \begin{pmatrix} 1\\ 2\end{pmatrix}= 2$$
Genauso gehe ich bei der Höhe \(h_B\) vor. Man erhält:
$$g_{hb}: \space \begin{pmatrix} 2\\ 1\end{pmatrix} \vec{x} = \begin{pmatrix} 2\\ 1\end{pmatrix} \cdot \begin{pmatrix} 7\\ -4\end{pmatrix}= 10$$ Der Schnittpunkt der beiden Geraden ist \(H\) - beide Geraden gemeinsam ergeben
$$\begin{pmatrix} 4& -1\\ 2 & 1\end{pmatrix} \vec{x}_H = \begin{pmatrix} 2\\ 10\end{pmatrix}$$ $$\Rightarrow \vec{x}_H = \begin{pmatrix} 2\\ 6\end{pmatrix}$$
Die Zeichnung bestätigt das Ergebnis
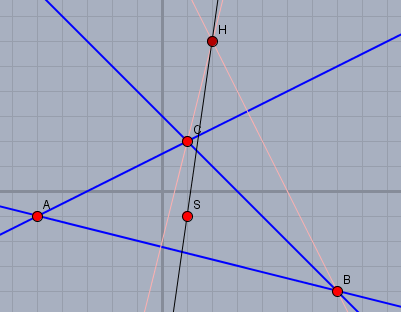
Die Eulergerade ist die Gerade durch die Punkte \(S\) und \(H\). Tipp: man erzeugt einen senkrechten Vektor indem man die Koordinaten vertauscht und eine von beiden negiert. Falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner