Mit Vektoren Eulersche Gerade berechnen

Question

Ich komm einfach nicht drauf. wie löst man das? bitte um hilfe. danke

Comments

1) wurde hier erledigt. https://www.mathelounge.de/514465/mit-vektoren-eulersche-gerade-bere… Resultat Schwerpunkt S = ( 1|-1)

Answer 1

Hallo Frido,

Eine Höhe steht senkrecht auf der dem Eckpunkt gegenüberliegenden Seite. Willst Du z.B. die Gerade $g_{hc}$, auf der $h_C$ liegt, bestimmen, so schaue Dir zunächst den Vektor $\vec{AB}$ an:

$$\vec{AB}= \begin{pmatrix} 7\\ -4\end{pmatrix} - \begin{pmatrix}-5 \\ -1\end{pmatrix} = \begin{pmatrix} 12\\ -3\end{pmatrix}$$ Dieser steht senkrecht auf der Höhe. Man kann ihn also sofort als Normalenvektor für die gesuchte Geradengleichung verwenden (Normalenform). $C= \begin{pmatrix} 1 & 2\end{pmatrix}^T$ liegt auf dieser Geraden, so lässt sich das $d$ in $\vec{n} \vec{x}=d$ berechnen. Vorher teile ich den Normalenvektor noch durch 3, da die Länge keine Rolle spielt $\vec{n} = \frac13 \begin{pmatrix} 12 & -3 \end{pmatrix} = \begin{pmatrix} 4 & -1 \end{pmatrix}$.

$$g_{hc}: \space \begin{pmatrix} 4\\ -1\end{pmatrix} \vec{x} = \begin{pmatrix} 4\\ -1\end{pmatrix} \cdot \begin{pmatrix} 1\\ 2\end{pmatrix}= 2$$

Genauso gehe ich bei der Höhe $h_B$ vor. Man erhält:

$$g_{hb}: \space \begin{pmatrix} 2\\ 1\end{pmatrix} \vec{x} = \begin{pmatrix} 2\\ 1\end{pmatrix} \cdot \begin{pmatrix} 7\\ -4\end{pmatrix}= 10$$ Der Schnittpunkt der beiden Geraden ist $H$ - beide Geraden gemeinsam ergeben

$$\begin{pmatrix} 4& -1\\ 2 & 1\end{pmatrix} \vec{x}_H = \begin{pmatrix} 2\\ 10\end{pmatrix}$$ $$\Rightarrow \vec{x}_H = \begin{pmatrix} 2\\ 6\end{pmatrix}$$

Die Zeichnung bestätigt das Ergebnis

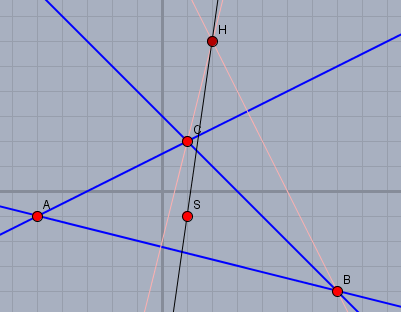
Die Eulergerade ist die Gerade durch die Punkte $S$ und $H$. Tipp: man erzeugt einen senkrechten Vektor indem man die Koordinaten vertauscht und eine von beiden negiert. Falls Du noch Fragen hast, so melde Dich bitte.

Gruß Werner