Hallo Exodius,
Nullstellen:
Multipliziere aus und fasse zusammen. Dann hast du eine biquadratische Gleichung ( nur die Potenzen x4 und x2 ), die du mit der Substitution z = x2 auf eine quadratische Gleichung reduzieren kannst:
z2 - 8·t2 ·z + 16 / t3 = 0 , Resubstitution ergibt dann die x-Werte
Extrema:
ft(x) = 1/8·t3·(x4 - 8·t2·x2) + 2
ft'(x) = t3 · x · (x2 - 4·t2) / 2 = 0 ⇔ x = 0 oder x = ± 2t
ft"(x) = t3·(3·x2 - 4·t2) / 2 → ft"(± 2t) = 4t5 > 0 → T1,2 ( ± 2t | 2 - 2·t7 )
H(0 | 2)
Ortskurven der Tiefunkte:
xT = ± 2t → t = ± x/2 , in y = 2 - 2t7
→ y = 2 ± x7 /64
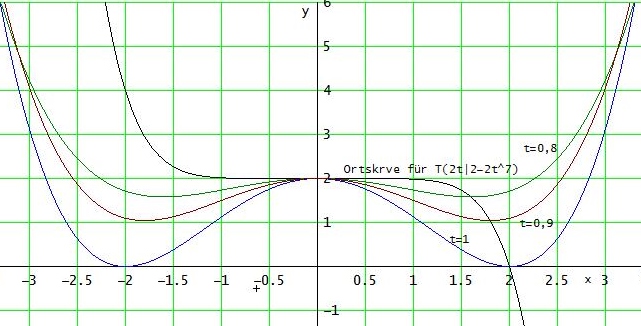
Es gibt also die Ortskurven y = 2 - x7/64 für die Tiefpunkte ( 2t | 2 - 2t7 ) [vgl. Bild]
und y = 2 + x7/64 für die Tiefpunkte ( -2t | 2 - 2t7 )
Gruß Wolfgang