Vorwort:
Eine Kugel ist ein geometrischer Körper, bei dem alle Punkte seiner Oberfläche den gleichen Abstand zu seinem Mittelpunkt haben. Es ist eine der wichtigsten geometrischen Figuren. Es gibt Fußbälle, Seifenblasen und noch viele weitere Gegenstände, die rund sind. Die wohl wichtigste uns bekannte Kugel ist unsere Erde, da jeder einzelne Mensch von Pythagoras bis Nelson Mandela auf ihr gedieht und die Welt, wenn auch nur ein bisschen, veränderte.
Dies ist der Grund, der uns dazu bewegt mal unser Sonnensystem genauer unter die Lupe zu nehmen. In diesem Artikel wirst du lernen wie man bei der Berrechnung einer Kugel vorgeht und dabei sogar noch was über die Astronomie lernen.
Das Schema der Kugelberechnung werden wir anhand dem Beispiel unseres direkten Nachbarn im Sonnensystem dem Mars erläutert.
Begriffserklärung und Aufbau:
Das ist der Mars:

Wir wollen alles über den Mars wissen, wissen jedoch noch nicht wie. Die Antwort auf dieses Problem ist sehr einfach. Obwohl die Kugel ein sehr komplexer und wichtiger Körper ist, sind die Berechnungen recht einfach! Doch vorab brauchen wir erst einmal die Formeln und müssen wissen, was man überhaupt alles ausrechnen kann.
Hier die Grafik einer Kugel:
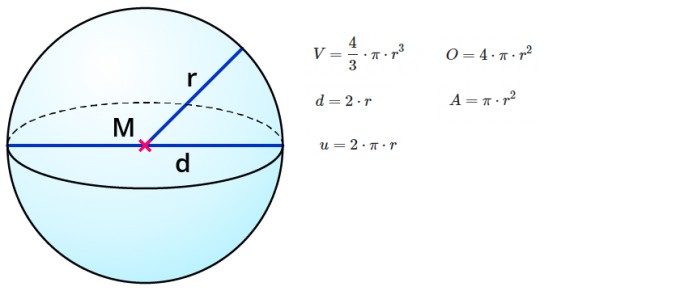
Wie man der Grafik entnehmen kann, kann man sehr viele Dinge recht einfach berechnen. Es gibt das Volumen(V), die Oberfläche(O), den Durchmesser(d), den Radius (r), die Kreisfläche(A) und den Umfang(u).
Wenn es euch wie mir geht; ihr nicht wisst was mit der Kreisfläche(A) gemeint ist, hier eine kleine Veranschaulichung:

Also um es auf unser Beispiel zu beziehen: Stellt euch einfach vor ihr würdet den Mars genau in der Mitte durchnschneiden und auf dessen Boden (farblich markiert) herumspazieren.
Anwendungsbeispiel:
Laut Wikipedia hat der Mars eine ungefähre Oberfläche(O) von 144.8 Millionen Kilometern. Beim Kreis brauchen wir glücklicherweise nur einen gegeben Wert, um die restlichen zu berechnen. Um den Radius zu berechnen, müssen wir uns nun eine Formel aussuchen bei der nur eine fehlende Variable zu finden ist, also:$$ O=4\cdot π \cdot r^2 $$ Gegeben haben wir die Oberfläche mit 144.800.000km und die Kreiszahl π. Formen wir also nun um:$$ O=4\cdot π \cdot r^2 \quad |÷4$$ Wir bringen zuerst die 4 mit der Divison auf die andere Seite:$$ \frac{O}{4}= π \cdot r^2 \quad |÷π$$ Anschließen bringen wir die Kreiszahl Pi auch per Division auf die andere Seite:$$ \frac{O}{4 \cdot π}=r^2 \quad | \sqrt{ } $$ Hierbei ist übrigens zu beachten, dass wenn man zwei Variablen/Zahlen via Division auf die andere Seite bringt sie sich unter dem Bruchstrich zusammen multiplizieren. Jetzt haben wir jedoch nicht das gewünschte r sondern r^2. Das ändern wir in dem wir die Wurzel auf der anderen Seite ziehen:$$r=\sqrt{\frac{O}{4 \cdotπ }} $$ Setzen wir dort nun unsere Werte ein:$$ r=\sqrt{\frac{144800000km^2}{4 \cdotπ }}\approx 3394.53km $$ Da wir nun den Radius des Planeten kennen, können wir auch die restlichen Werte ermitteln:$$ d=2 \cdot 3394.53km \approx 6789.06km$$$$V=\frac{4}{3}\cdot π \cdot 3394.53^3km \approx 1.638 \cdot 10{}^{11}km^3 $$$$u=2 \cdot π \cdot 3394.53km \approx 21328.46km $$$$A=π \cdot 3394.53^2km \approx 36200050.39km^2$$ Und da wir uns jetzt noch viel mehr für den Mars interessieren wollen wir auch noch wissen wie schwer der Mars eigentlich ist. Da wir keine Waage benutzen können ist es hilfreich zu wissen welche Dichte der Mars hat. Laut Wikipedia hat der Mars eine Dichte von 3.93 g/cm^3 d.h. wir können mit diesem Wert das Gewicht vom Mars berechnen. Das geht wie folgt: Zuerst müssen wir das Volumen auf cm^3 bringen.$$1.638 \cdot 10{}^{11}km^3\quad ⟹1.638 \cdot 10{}^{26}cm^3$$ Nun können wir also das Gewicht berechnen:$$1.638 \cdot 10{}^{26}cm^3 \cdot 3.93\frac{g}{cm^3} \approx 6.44 \cdot 10{}^{26}g\quad ⟹ 6.437 \cdot 10{}^{11} Gt $$ (Gt=Gigatonnen)
Nun haben wir schon ziemlich viel über den Mars gelernt! Wenn du Lust hast kannst du hier auch noch einmal versuchen die Venus auszurechnen:
Durchmesser(d)=12,104 km
Hiermit kannst du ebenfalls alle Werte, die ich berechnet habe auch ausrechnen! Gutes gelingen.
Es werden in dieser Artikelreihe noch folgende Körper aufgeführt:
Die Pyramide, der Zylinder und der Kegel.