ich habe folgende Matrix und will die Eigenwerte berechnen. Leider konnte ich es mal und momentan funktioniert es nicht mehr. Ich hänge an der Stelle, dass ich mir die Matrix vorbereitet habe um daraus das Polynom abzuleiten, welches ich dann Null setzen kann. Dann möchte ich die Determinante mit Laplace berechnen ...
geg:
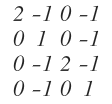
jetzt Determinante bestimmen
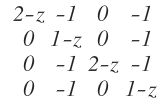
jetzt mein Fehler .. ich komme auf
(2-z)²(1-z)²-1 =0
das stimmt aber nicht, weil ich damit nicht auf die richtigen Eigenwerte komme. Bin über jeder Hilfe dankbar