Stetigkeit, Differenzierbarkeit einer Betragsfunktion

Question

habe die Aufgabe f(x) = |x-2| (die Striche sollen einen Betrag darstellen)

Ich soll diese sowohl auf Stetigkeit, als auch auf Differenzierbarkeit überprüfen.

Wie funktioniert das ?

MfG

Answer 1

Die Funktion ist stetig da keine Polstelle,
Lücke, Division durch 0 vorhanden ist.

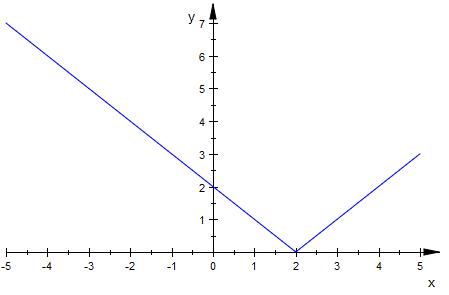
f(x) = |x-2| bedeutet
für x- 2 ≥ 0 => x ≥ 2
f1 ( x ) = x -2

für x- 2 < 0 => x < 2
f2 ( x ) = ( x -2 ) * -1
f2 ( x ) = -x + 2

f1 ´( x ) = 1
f2 ´( x ) = -1

Die Steigung bis zur Stelle x = 2
ist -1 ( fallend ), dann 1 steigend.

Die Funktion ist nicht differenzierbar.

Comments

Ist jede Betragsfunktion nicht differenzierbar oder nur diese ?

---

Da habe ich mir noch keine Gedanken
drum gemacht.
Ich denke aber jede.

---

Die Funktion ist stetig da keine Polstelle,
Lücke, Division durch 0 vorhanden ist.
Wieder eine deiner eigenen Definitionen?

---

Hallo Georg,

an einer Polstelle wäre eine Funktion f nicht definiert.

Für x ∉ D_f  stellt sich die Frage nach der Stetigkeit nicht.

----

die Funktion  f: ℝ → ℝ  ,  f(x) = | x³ |   

ist in ganz ℝ  differenzierbar