Erkennen von Exponentialfunktionen in Graphen

Question

auf dem unten abfotografierten Bild gehört die Formel -x+1 zu Graph 2, 1-8/5x zu Graph 1 und 2-0,9x zu Graph 3.

Meine Frage ist, wie erkenne ich das denn? Was kann ich aus den Formeln erschließen, sodass ich die Formel habe, ich bitte um eine ausführliche Erklärung. 

Answer 1

einmal kannst du sehen, dass die Funktion gespiegelt ist. Das heißt, die Funktionen müssen so lauten:

f(x)=a•b^{-x}

Zuerst zum Graph 7 (Grün)

Du musst jetzt Steigungsdreiecke dir denken.

Schauen wir mal nach markanten Punkten.

Bei x=0 kommt 1 raus.

Bei x=1 kommt 4 raus.

Daraus folgt, dass es sich immer viertelt, da wir ja eigentlich von der anderen Seite ausrechnen. 

Also: $$f(x)={4}^{-x}$$oder man kann es auch umschreiben in $$\frac{1}{4^x}$$Da wird auch klar, was ich oben gemeint habe. Je größer der x-Wert, umso kleiner der y-Wert.

Bei Graph 6 fällt mir spontan auch nichts ein, aber zur Kontrollen von Graph 7

~plot~ 4^{-x};1/(4^x) ~plot~

Du siehst auch, dass beide das Gleiche ergeben.

Wenn mir noch was einfällt, schreibe ich es in die Kommentare. Vielleicht bekommst du anderen auch alleine hin.

Gruß

Smitty

Answer 2

Hallo Mathenoob,

y = - x + 1  [G2]   und   y = -0,9x + 2  [G3]   (2-0,9x)

sind Geradengleichungen der Form y = mx +

Die Geraden gehen durch (0 | n)   und haben die Steigung m 

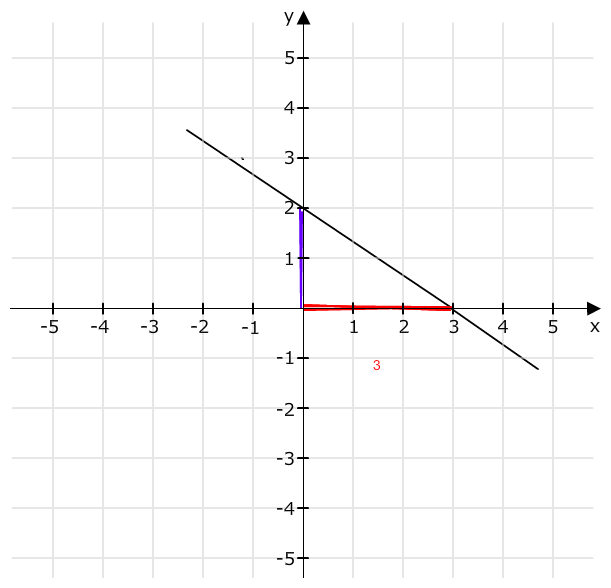
Beispiel im Bild:  Die Gerade fällt, also ist m negativ  m = - 2/3 

Die Gerade geht durch (0|2)  →  n = 2  

y = -2/3 x + 2  

m = - 1/1 = -1  bei G2  und   m = - 2 / 2,2  ≈ - 0,9  bei G3  kommt etwa hin

und die Achsenschnittpunkte stimmen auch.  

 

Mit  y = 1 - 8/5x   kann ich leider überhaupt  nichts anfangen. Wie immer ich es interpretiere ergibt sich nichts in deinem Bild Brauchbares:  

So wie es dasteht,  wäre es eine Gerade durch (0|1) mit der Steigung -8/5, passt nicht 

y = 1 - 8 / 5^x   hätte x=1 einen negativen y-Wert, passt auch nicht .

y = 1 - 8/(5x)  ebenfalls

Gruß Wolfgang