Hallo Maron,
a) und c)
Jeder Puck mit dem Radius r "blockiert" auf der Grundfläche der Schachtel eine Quadratfläche AB mit der Kantenlänge 2r.
Das ergibt eine freie Fläche AF = (2r)2 - π r2 = 4 r2 - π r2 = (4 - π) · r2 ≈ 0,858 r2
Der prozentuale Anteil der freien Fläche ist also 0,858 r2 / (π r2) ≈ 0,273 = 27,3 %
Das Luftvolumen beträgt deshalb ebenfalls 27,3 %, weil bei Luftanteil und Puck einfach mit h multipliziert wird.
b)
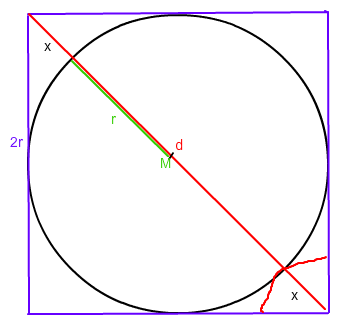
x ist der Radius des kleinen Kreises in der Mitte des gegebenen Bildes.
d die Diagonale des Quadrats.
d2 = (2r)2 + (2r)2 = 8r2 → d = √8 ·r = 2r + 2x
→ x = 1/2 · (√8 - 2 ) · r = (√2 - 1) · r ≈ 0,414 r
Gruß Wolfgang