folgende Funktionen sind gegeben:

zu folgender Zusammensetzung lautet das Ergebnis "1" : 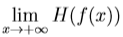
Ich komme dort aber nur auf "0". Denn der Grenzwert zu f(x) ist "0"?! Und H(0) = 0!
Wahrscheinlich ist die Lösung ganz einfach aber ich verstehe es einfach nicht. Bitte um einen kurzen Ratschlag.
Danke.