kann mir vielleicht jemand helfen Bzw. sagen, ob ich die folgende Aufgabe richtig löse?
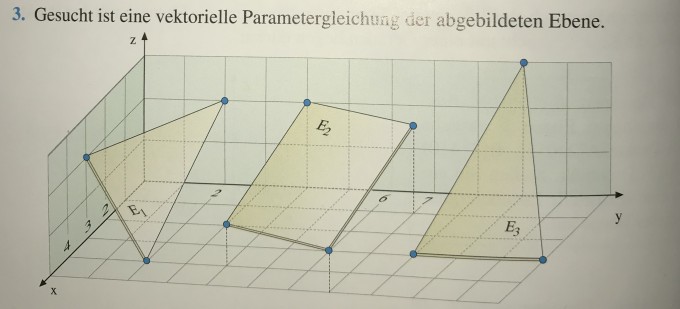
Aufgabe: Gesucht ist eine vektorielle Parametergleichung der abgebildeteten Ebene (siehe Bild)
Mein Ansatz:
Die Punkte der Ebenen ablesen und dann die Differenzvektoren mit den Punkten bestimmen
E1:
A(4|2|0) B(0|2|2) C(3|0|2)
AB= (-4 0 2)
AC= (-1 -2 2)
x= (4 2 0) +r*(-4 0 2) +s(-1 -2 2)
Bei den beiden anderen Aufgaben komm ich nicht weiter. Entstehen eigentlich nicht unterschiedliche Lösungen, weil man auch die Punkte der Ebenen unterschiedlich ablesen kann?
Vielen Dank