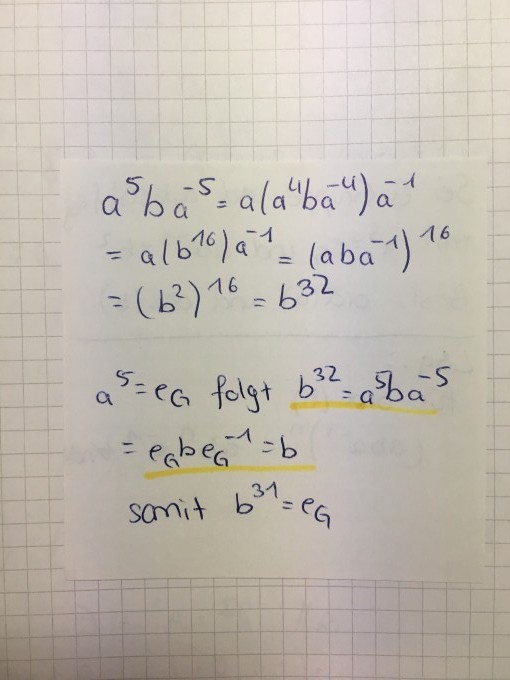Ordnung Algebra von b^2?

Question

ich habe hier diese Aufgabe. Die Ordnung von a kann ich berechnen. Bei b scheitere ich leider.

In der Lösung wird mit diesem Ansatz angefangen bis a^5 wird das durchgerechnet . Allerdings verstehe ich nicht warum der Exponent n nur auf das b geht?

am Schluss steht dann noch, dass b^31 das neutral Element ist. Wird dann einfach im Schritt davor durch b dividiert ?

Answer 1

Tipp1: Für \(n=2\) gilt \(\ (aba^{-1})^2=(aba^{-1})(aba^{-1})=(ab)\underbrace{(a^{-1}a)}_{=e_G}(ba^{-1})=ab^2a^{-1}\).
Induktiv folgt \((aba^{-1})^n=ab^na^{-1}\).
Tipp2: Es wurde mit \(b^{-1}\) multipliziert.

Comments

super vielen Dank!!! Habe eben noch mal alles durchgerechnet und habe es nun auch verstanden