Ortskurve der Hochpunkte für fa(x)=150a^{2}*x*e^{-0,2ax}

Question

die Frage steht oben, komme leider nicht auf das Ergebnis. & MfG !

Answer 1

f ( x ) = 150*a^2 * x * e^{-0.2*a*x}
f ´( x ) = -a^2 * e^{-0.2*a*x} * ( 30.0*a*x - 150.0)

f ´( x ) = 0
Hochpunkt bei
x = 5 / a

a = 5 / x
in f eingesetzt
ort ( x ) = 1379.547904 / x

Die Lösung wurde graphisch überprüft
und stimmt.

Bei Bedarf nachfragen.

Comments

Also auf 5/a komme ich ebenfalls, jedoch nachdem ich das in fa(5/a) einsetze, kriege ich nur seltsame Ergebnisse :/

Danke für die Angabe der Ortskurve !

---

f (x) = 150*a^2 * x * e^{-0.2*a*x}
wenn du x = 5  / a einsetzt bekommst du
den Funktionswert des Hochpunkts heraus.
Den brauchen wir nicht. ***

x = 5 / a
Umstellen zu
a = 5 / x und einsetzen
150*a^2 * x * e^{-0.2*a*x}
150 *(5/x) ^2 * x * e ^{-0.2*(5/x)*x}
ort ( x ) = 3750 / x * e ^{-1}
ort ( x ) = 1379.547904 / x

***
Es ist ein bißchen kompliziert
f (x) = 150*a^2 * x * e^{-0.2*a*x}
wenn du x = 5  / a einsetzt bekommst du
f ( a ) heraus.
Auf der x-Achse ist aber x und nicht a
deshalb brauchen wir
ort ( x )

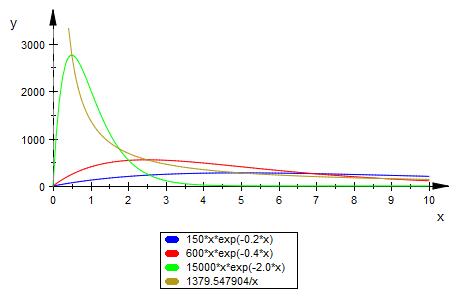blau, rot, grün : 3 Kurven der Kurvenschar fa
oker : Ortskurve der Hochpunkte

Answer 2

Die Nullstellen der ersten Ableiung heißen x=5/a und für positive a sind dort Hochpunkte. Ersetze also a in der Funktionenschar durch 5/x, dann erhältst du die Gleichung der Ortskurve.