Ich nehme an, dass die 4.6cm für die gesamte Strecke steht. Und durch zwei geteilt werden kann. Hier damit wir nicht aneinander vorbeisprechen.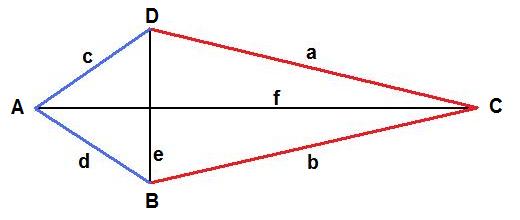
Oben (der blau markierte Teil) bestehend aus zwei rechtwinkligen Dreiecken bildet ein gleichschenkliges Dreieck mit den Schenkeln c und d, welche gleich lang sind. Außerdem ist die Strecke von B nach D gegeben mit 4.6cm. Der Winkel Gamma ist also:$$ \gamma=arccos\left(\frac{2\cdot 3^2 -4.6^2}{2 \cdot 3^2}\right)≈ 100.11° $$
Die Hälfte des Winkels β und das was rechts ist (erkenne ich nicht) können wir so berechnen:$$ \alpha=\beta=arccos\left(\frac{4.6}{2\cdot 3}\right)≈ 39.95° $$ Gehen wir nun zum anderen Dreieck über (rot-markiert). Dort haben wir die Grundseite gegeben und a=b, da es wieder gleischenklig ist:$$ \alpha=\beta=arccos\left(\frac{4.6}{2\cdot 6}\right)≈ 67.46° $$ und der Winkel Gamma:$$\gamma=arccos\left(\frac{2\cdot 6^2 -4.6^2}{2 \cdot 6^2}\right)≈ 45.08°$$ Wir müssen die beiden Teilwinkel zusammenrechnen: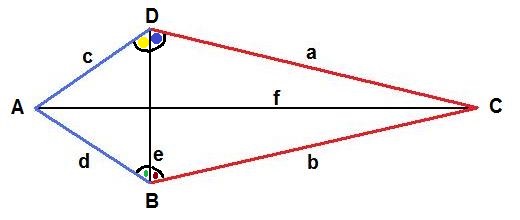
Unter Teilwinkel verstehe ich die hier (rot, grün, gelb und lila markierten) Punkte, welche zwei ganze Winkel bilden!
$$ \delta, \beta=39.95°+67.46° =107.41° $$ Zusammen müssten alle Winkel 360° ergeben:$$ 2\cdot 107.41+45.08+100.11=360.01 $$ Also richtig, nur ein winziger Rundungsfehler...