der graph einer ganzrationalen funktion 4. grades ist symmetrisch zur 2. achse,
f(x) = ax^4 + bx^2 + c
hat t(2;4) als tiefpunkt
f(2) = 4
16·a + 4·b + c = 4
f'(2) = 0
32·a + 4·b = 0
und schliesst mit der tangente durch t eine flaeche mit dem inhalt 256/15 ein.
F(2) = 128/15
a/5·x^5 + b/3·x^3 + c·x = 128/15
32·a/5 + 8·b/3 + 2·c = 128/15
48·a + 20·b + 15·c = 64
Das LGS hat die Lösung a = 1/32 ∧ b = - 1/4 ∧ c = 9/2
f(x) = 1/32·x^4 - 1/4·x^2 + 9/2
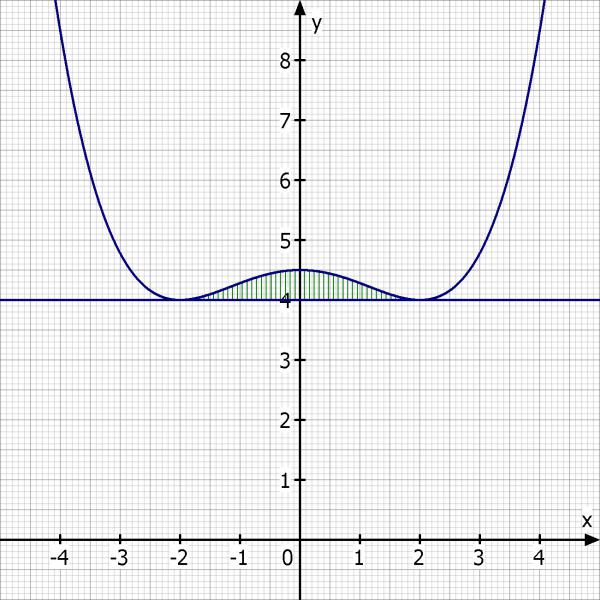
Skizze: