Hallo moonlight,
wieder mal 'ne schöne Geometrie-Aufgabe ...
Ich kann doch die Aufgabe auch mit dem Peripheriewinkelsatz lösen, oder?
Ja - kannst Du. Dazu zeichne ich zunächst einen der Peripheriewinkel ein, z.B. den blauen Winkel beim Punkt \(D\).
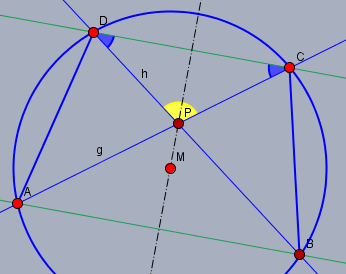
Der blaue Winkel bei \(D\) ist Peripheriewinkel über der Sehne \(BC\). Dieser Winkel ist also unabhängig von der Lage von \(BC\) zum Punkt \(D\). Auf Grund der (Achsen-)Symmetrie bezüglich der Geraden durch den Schnittpunkt \(P\) von \(g\) und \(h\) und \(M\) (dem Mittelpunkt des Kreises), muss der blaue Winkel bei \(C\) identisch zum Winkel bei \(D\) sein. Oder - alternative Begründung: Der blaue Winkel bei \(C\) ist Peripheriewinkel über der Sehne \(AD\), die die Länge von \(BC\) im selben Kreis hat, und muss demzufolge gleich groß zu dem Winkel bei \(D\) sein.
D.h. die Winkel im Dreieck \(\triangle PCD\) sind unabhängig von der Lage der Sehne \(BC\) zu \(AD\). Der gelbe Winkel bei \(P\), unter dem sich die Geraden \(g\) und \(h\) schneiden, ist folglich ebenso unabhängig von der Lage der beiden Sehnen \(BC\) und \(AD\).
Gruß Werner