Grafisch die Zeit bestimmen, bei der beide Kanister gleich voll sind

Question

Ich habe eine Textaufgabe vorliegen. Die Ergebnisse sollen grafisch im Koordinatensystem dargestellt werden.

Die Aufgabe lautet:

Zwei gleiche Kanister werden mit Benzin gefüllt. Der erste mit 20ml pro Minute und der zweite, mit Abstand von 3 Minuten, später zu füllen begonnen. Da aber mit 50ml pri Minute.

Es soll grafisch die Zeit bestimmt werden, bei der beide Kanister gleich voll sind.

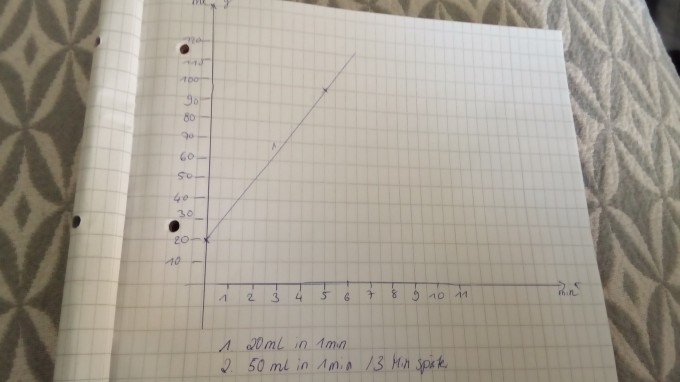
Ich habe ein Koordinatensystem gezeichnet.

x= Minuten und y=Milliliter

Punkt eins bei 20ml gesetzt und Punkt zwei bei 5 minuten und 100ml

Aber wie Handhabe ich das mit Gefäß 2, welches 3 Minuten später gefüllt wird und mit50 ml je Minute?

Wäre schön wenn mir jemand helfen könnte.

Answer 1

Der erste Kanister hat am Anfang 0 ml und erst nach einer Minute 20.

Die Gerade beginnt also in (0;0) und geht durch (1;20).

Der zweite ist nach 3 min noch bei 0 und steigt dann  um 50 pro MInute,

ist also bei MInute 4 auf der Höhe von 50.

Am Ende von Minute 5 sind beide gleichweit gefüllt ( 100 ml)

~plot~ 20x;-150+50x; [[0|10|0|200]] ~plot~

Answer 2

Hallo Wonne,

der erste Kanister ist am Anfang (also zum Zeitpunkt \(x=0\)) leer. Folglich geht die lineare Funktion, die die Benzinmenge im Kanister 1 anzeigt, durch den Ursprung. Der zweite Kanister ist zum Zeitpunkt \(t=3\text{min}\) leer. Dann muss seine lineare Funktion durch den Punkt \((3\text{min}; 0 \text{ml})\) gehen. So sieht das als Graph aus:

~plot~ 20x;50*(x-3);[[-1|10|-5|160]] ~plot~

Du siehst dort, dass sich beide linearen Funktionen bei \((5 \text{min}; 100 \text{ml})\) treffen. Im einzelnen lauten sie: $$\begin{aligned} y_1(x) &= 20 \frac{\text{ml}}{\text{min}} x \\ y_2(x) &= 50 \frac{\text{ml}}{\text{min}} (x - 3 \text{min}) = 50 \frac{\text{ml}}{\text{min}} x - 150 \text{ml}\end{aligned}$$ Setzt Du in beide Funktionen \(5\text{min}\) ein, so erhältst Du in jedem Fall \(100 \text{ml}\).

Gruß Werner