Also es gibt zwei Möglichkeiten
1.
U = a + 2b = 100 mit a <= 40 --> b = 50 - a/2
A = a·b = a·(50 - a/2) = 50·a - 0.5·a^2
A' = 50 - a = 0 --> a = 50
50 liegt nicht im Definitionsbereich damit ist hier a = 40 ein Randextremum.
2.
U = a + (a - 40) + 2b = 100 mit a >= 40 --> b = 70 - a
A = a·b = a·(70 - a) = 70·a - a^2
A' = 70 - 2·a = 0 --> a = 35
35 liegt nicht im Definitionsbereich damit ist hier a = 40 ein Randextremum.
Wir zeichnen die beiden Graphen der Fläche in Abhängigkeit von a in ein Koordinatensystem.
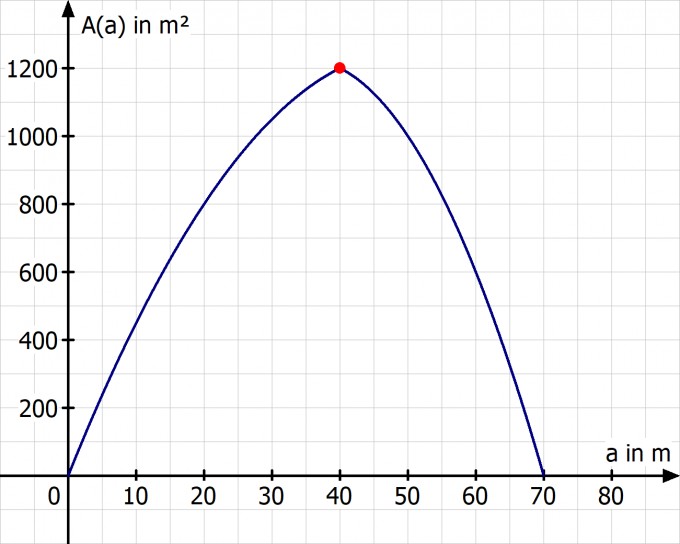
Hier kann man das Maximum recht gut sehen.