Schau Dir mal folgene Skizze an.
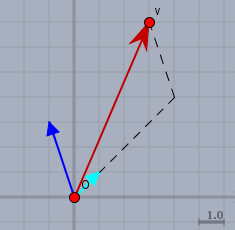
Dort ist ein Vektor \(v\) (rot), der in den kartesischen Koordinaten (System \(B_1\)) die Position \(^{1}v=(3 \,\, 7)^T\) hat. Die beiden blauen Vektoren sind die Basisvektoren eines Systems \(B_2\). Die Transformationsmatrix \(B_1 \to B_2\) lautet in diesem Fall
$$^2T_1 = \begin{pmatrix}0.75& 0.25\\ -0.25& 0.25\end{pmatrix}$$
Du erhältst den Vektor \(^2v\) im System \(B_2\), indem Du die Matrix \(^2T_1\) mit dem Vektor \(^1v\) multiplizierst. Es ist
$$^2v= \, ^2T_1 \cdot \, ^1v = \begin{pmatrix}0.75& 0.25\\ -0.25& 0.25\end{pmatrix} \cdot \begin{pmatrix}3\\ 7\end{pmatrix} = \begin{pmatrix}4\\ 1\end{pmatrix}$$
D.h. wenn Du mit dem hellblauen Vektor 4-mal in seine Richtung marschierst und dann einmal den dunkelblauen hinzufügst, so kommst Du wieder bei \(v\) raus.
Noch ein Tipp: Das Inverse der Matrix \(\left( \, ^2T_1\right)^{-1} = \, ^1T_2\) ist
$$\left( \, ^2T_1\right)^{-1} = \begin{pmatrix}0.75& 0.25\\ -0.25& 0.25\end{pmatrix}^{-1}= \begin{pmatrix}1& -1\\ 1& 3\end{pmatrix} = \,^1T_2$$
In den Spalten dieser Matrix findest Du die (blauen) Basisvektoren des Systems \(B_2\) wieder, so wie sie in \(B_1\) beschrieben sind. Multiplizierst Du diese Matrix mit \(^2v\) erhältst den Vektor in den ursprünglichen Koordinaten zurück:
$$^1T_2 \cdot \, ^2v = \,^1v $$ probier's mal aus.