Wendet man das totales Differential an, wenn man eine Funktion hat, in der sowohl eigene Funktionen als auch einzelne Variablen vorhanden sind? Dass man also das einfache Differential und das partielle Differential verbinden?
Kenne die Formel wie folgt:
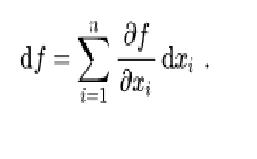
Also die Summe aus dem Produkt der partiellen und der einfachen Ableitungen einer Variablen.
In der Aufgabe die ich gerade bearbeite gibt es folgende Funktion für den Output einer VW:
Y = C(Y-T)+I(r)+G
Um die Beziehung von r und Y zu erfahren wurde das totale Differential angewendet (wieso?)
Das wurde folgendermaßen notiert:
1*dY = C'(Y-T)*1+dY+C'(Y-T)*(-1)*dT+I'(r)*dr+1*dG
Was hat die "1" zu bedeuten?