Produkt von Matrizen berechnen

Question

Aufgabe:

Gegeben seien die folgenden Matrizen:

\( \mathbf{A}=\left[\begin{array}{ccc}-1 & -3 & -9 \\ 5 & 1 & -5\end{array}\right] \quad \mathbf{B}=\left[\begin{array}{cc}-3 & -7 \\ -8 & -7 \\ -3 & 7\end{array}\right] \quad \mathbf{C}=\left[\begin{array}{ccc}-5 & -8 & -2 \\ 8 & -3 & 8\end{array}\right] \)

Berechnen Sie den folgenden Ausdruck.

\( 3 \mathbf{A}^{T}-5 \mathbf{B}+5 \mathbf{C}^{T}= \)

Ich soll nun folgenden Ausdruck berechnen: 3A(transponiert)-5B+5C(transponiert)

Transponieren ist natürlich klar.

Ich habe ein Ergebnis vorliegen: [-13,-9,-22; 90,23,-10]

Weiß jedoch nicht mehr, wie ich dahin gekommen bin und finde auch keinen Lösungsweg zu diesem Ergebnis.

Answer 1

Hallo Maxi,

Weiß jedoch nicht mehr wie ich dahin gekommen bin ...

Das Multiplizeren einer Matrix mit einer Zahl und das Addieren von Matrizen sollte doch kein Problem sein. Was genau weißt Du da nicht?

Ach und wieso kann man keine Grafiken mehr hochladen? Bei der Veranschaulichung von z.B. Matrizen ist dies deutlich übersichtlicher..

Nutze den LaTeX-Assistenten (rechts bei den Eingabetools). Dann sähe das so aus:

$$A = \begin{pmatrix} -1 & 5 \\ -3 & 1 \\ -9 & -5 \end{pmatrix} \quad A^T= \begin{pmatrix} -1&-3&-9 \\ 5&1&-5 \end{pmatrix} \\ B = \begin{pmatrix} -3& -8& -3 \\ -7&-7&7 \end{pmatrix} \\ C = \begin{pmatrix} -5&8 \\ -8&-3 \\ -2&8 \end{pmatrix} \quad C^T= \begin{pmatrix} -5&-8&-2 \\ 8&-3&8 \end{pmatrix}$$

... und das muss man nur noch richtig abschreiben, und ein bißchen mal, plus und minus:

$$3A^T-5B+5C^T \\ \begin{aligned} \space &= \begin{pmatrix} -3&-9&-27 \\ 15&3&-15 \end{pmatrix} - \begin{pmatrix} -15& -40& -15 \\ -35&-35&35 \end{pmatrix} + \begin{pmatrix} -25&-40&-10 \\ 40&-15&40 \end{pmatrix} \\ &= \begin{pmatrix} -13 & -9 & -22 \\ 90 & 23 & -10 \end{pmatrix}\end{aligned}$$

Answer 2

A= [-1 , 5 ; -3 , 1; -9 , -5] ; B= [-3, -8, -3; -7,-7,7] und C= [-5,8 ; -8,-3; -2,8]

Ich soll nun folgenden Ausdruck berechnen: 3A(transponiert)-5B+5C(transponiert)

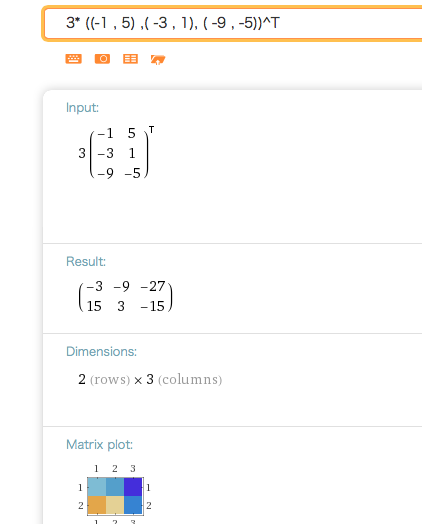
= 3  [-1 , 5 ; -3 , 1; -9 , -5]^T  - 5 [-3, -8, -3; -7,-7,7] + 5 [-5,8 ; -8,-3; -2,8]^T

= ( (-3, 15), (-9, 3), (-27, -15))^T + ((15, 40, 15),(35,35,-35)) + ((-25, 40), (-40,-15),(-10,40))^T

Nun nachrechnen (berichtigen, wenn nötig), transponieren, wo verlangt, und dann komponentenweise die Matrizen addieren.

https://www.wolframalpha.com/input/?i=3*+((-1+,+5)+,(+-3+,+1),+(+-9+,+-5))%5ET

Hier kannst du dir schrittweise die Summanden berechnen lassen.