Diese Aufgabe spiegelt schön die Geschichte der Mathematik wieder.
Wenn Dir -1.54 reichen, dann bist Du etwa 500 bis 600 Jahre zurück oder in einer unteren Klasse, die einfach nur
a) 1 Bild malt und den Wert grob abließt. (oder
b) mit Probieren {Bisektion} nach 3 Schritten endest)
pq-Formel ist für Polynome vom Grad 2 und wir haben aber hier Grad 3.
c)
https://de.wikipedia.org/wiki/Newton-Verfahren
war schon vor dem Jahr 1700 bekannt und ist mit 4 Schritten etwa 10 Stellen genau.
d)
https://archive.lib.msu.edu/crcmath/math/math/v/v082.htm
ist schon über 200 Jahre bekannt für diese Art der Spezialfälle.
(siehe Kommentar von nn oben)
e) https://de.wikipedia.org/wiki/Cardanische_Formeln
kennt man auch schon im 17. Jh., hat aber noch Fallunterscheidungen.
f) Diese Fallunterscheidungen wurden mit den komplexen Zahlen eliminiert und seit über 90 Jahren
kennt man die exakten expliziten Formeln für Polynome vom Grad 3: PQRST-Formel
http://www.lamprechts.de/gerd/Quartische_Gleichung.html
Ein online Rechner für e) und f) findet man unter
http://www.lamprechts.de/gerd/php/gleichung-6-grades.php
ergibt die 3 Lösungen im Bild
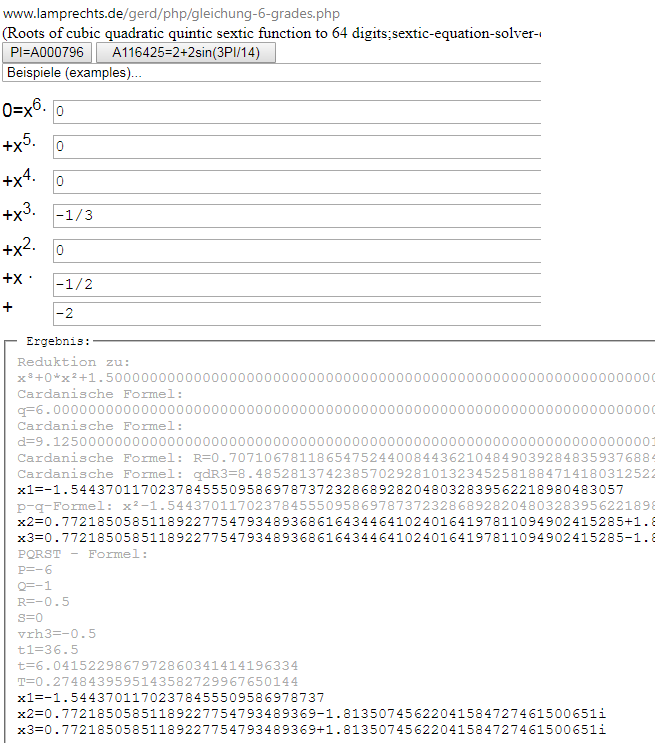
x1 ausgeschrieben: (sqrt(146) - 12)^{1/3}/2^{2/3} - 1/(2 (sqrt(146) - 12))^{1/3} = -1.54437011702378455509586978737...
mit sqrt(x)=Wurzel(x) und x^{1/3}= 3. Wurzel von x