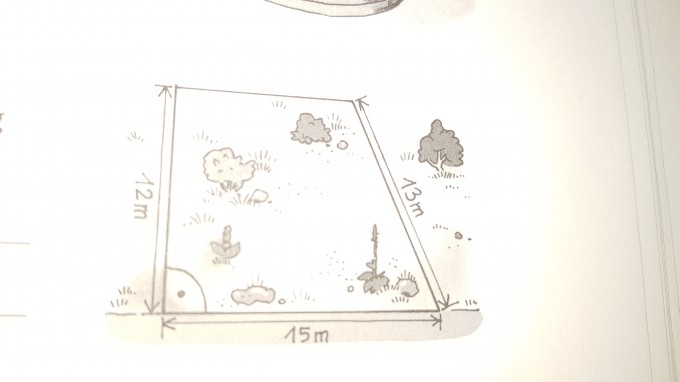
bitte um Hilfe. Bei der Berechnung der Diagonalen nutze ich den Pythagoras und rechne:
C2=(12)2 + (15)2 C= 19,2m.
Für die 2.Diagonale benutze ich den Sinussatz, um Winkel Gamma zu errechnen, also
13/15 = sin 45°/ Gamma
Gamma = 13 × sin 45° / 15 = 35,1°
Jetzt kann ich Winkel Beta ausrechnen = 91,9° und anschließend die Diagonale berechnen:
a/b=sinAlpha/ ein Beta
b= 13 × sin 91,9° / sin 45°= 18,4m
Ist mein Rechenweg richtig? Das Ergebnis stimmt irgendwie nicht mit der Zeichnung überein.