Punkt F auf der Kante einer Pyramide bestimmen

Question

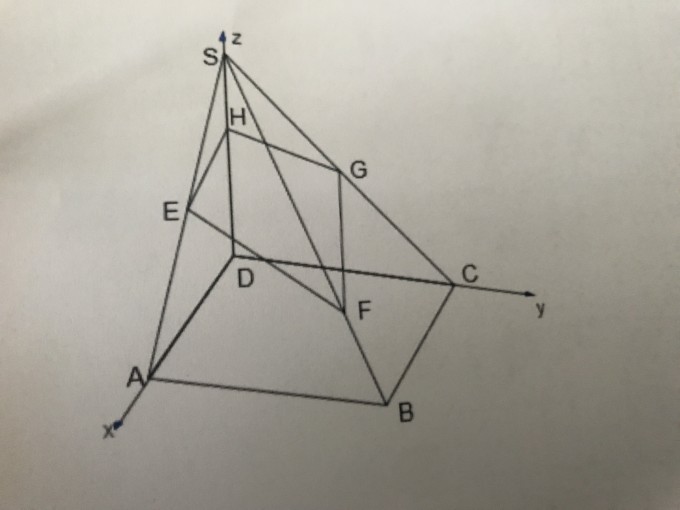
ich habe eine schiefe Pyramide gegeben mit den Punkten:

A(8,0,0)

B(0,8,0)

D(0,0,0)

S(0,0,8)

E(4,0,4)

G(0,4,4)

H(0,0,5)

Nun soll ich den Punkt F der Ebene EGF berechnen!

Normalerweise könnte man ja sagen:

F = S + SH

Da aber scheinbar H und F nicht auf einer Ebene liegen geht das ja nicht!

Ich verstehe nicht ganz wie ich sonst auf die Koordinaten von F kommen soll!

Ich könnte ja ansonsten noch die Ebene aufstellen:

E: x = E + r* EG + s* EF

Aber da fehlen mir ja neben F noch r und s!

Außerdem einen weiteren Punkt , welcher auf der Ebene liegt zum gleich setzen!

Wäre nett wenn mir da mal jemand helfen könnte, mir gehen echt die Ideen aus

 jh

EDIT: Kopie aus Kommentar:

Die Grundfläche einer (schiefen) Pyramide besitzt die Eckpunkte A(8,0,0);B(0,8,0);D(0,0,0), ihre Spitze sei der Punkt S(0,0,8). Die Ebene E_EGH wird festgelegt durch die Punkte E(4,0,4); G(0,4,4) und H(0,0,5). Geben Sie die Punktrichtungsform und die Punktnormalform der Ebene E_EGH an. Bestimmen Sie die Koordinaten des Punktes F der Ebene E_EGH.

Comments

F = S +  t SH, wobei t ∈ ℝ. Genauer 0 < t < 1. 

Ist EFGH kein "flaches" Viereck?

Wenn EFGH flach ist, kannst du die Ebene durch E, G und H mit der Geraden durch B und S schneiden. -> F.

---

Danke schonmal für die Antwort!

Genau die Information ist eben nicht in der Aufgabe gegeben, daher hab ich auch das Problem. Wenn EFGH flach ist, wäre es kein Problem!

Von der Zeichnung her bin ich jetzt davon ausgegangen, dass der Punkt F tiefer liegt als der Punkt H! Daher versteh ich nicht ganz wie man in dem Fall auf F kommen soll!

---

mir scheint es ist nur eine optische Täuschung und EFGH ist flach, und F muß etwas tiefer liegen, da H höher als EG liegt.

---

Okay dann ist es leicht! War deswegen die ganze Zeit total verwirrt! Dann geh ich mal davon aus, dass H und F die selbe Höhe haben

---

Wenn H und F dieselbe höhe hätten, dann wäre EFGH keine Ebene, denn H liegt höher als E und G. Genau genommen ist EFGH nicht flach sondern eine schiefe Ebene.

---

Und wie bestimmt man dann in dem Fall Punkt F?

Answer 1

F = S +  t SH, wobei t ∈ ℝ. Genauer 0 < t < 1. 

Ist EFGH kein "flaches" Viereck?

Wenn EFGH flach ist, kannst du die Ebene durch E, G und H mit der Geraden durch B und S schneiden. -> F.

Sorry: Ich habe mich missverständlich ausgedrückt.

Ich hätte besser geschrieben

Wenn EFGH eben ist (d.h. E,F,G und H liegen in derselben (schiefen) Ebene, kannst du die Ebene durch E, G und H mit der Geraden durch B und S schneiden. -> F.

Das ist vermutlich schon der Fall. Das Viereck ist eben (nicht gebogen wie ein Zelt oder so was). Sonst müsste das in der Fragestellung stehen.

Comments

Okay jetzt hab ichs! Dankeschön

---

Bitte. Konntest du das Resultat irgendwie überprüfen?

Answer 2

Dein Planfigur ist falsch, B und C sind vertauscht?

Sollte F nicht durch die Ebene EHG beschrieben werden?

Dann F=(6,6,2)

Wie heißt die Original Aufgabe? ergibt so keinen Sinn...

Comments

Also die Aufgabe lautet:

Die Grundfläche einer (schiefen) Pyramide besitzt die Eckpunkte A(8,0,0);B(0,8,0);D(0,0,0), ihre Spitze sei der Punkt S(0,0,8). Die Ebene E_EGH wird festgelegt durch die Punkte E(4,0,4); G(0,4,4) und H(0,0,5). Geben Sie die Punktrichtungsform und die Punktnormalform der Ebene E_EGH an. Bestimmen Sie die Koordinaten des Punktes F der Ebene E_EGH.

Stimmt da hab ich mich mit der Ebenenbezeichnung vertippt

---

Nicht nur, B hat in Deiner Zeichnung vermutlich die Koordinaten (8,8,0) und nicht (0,8,0) wie in Deiner Angabe....

---

@Wächter. Dann ist aber auch G falsch.

---

Kommt drauf an, welche Annahmen die fehlenden und falschen Informationen ersetzen...

Ich arbeite mit diesen Werten:

Dann stimmt aber die Nummerierung nicht, aber Namen sind Schall und Rauch...