ich bin gerade dabei einige Extremwertaufgaben durchzurechnen!
Ich habe aber 2 Aufgaben bei denen ich etwas ratlos bin!
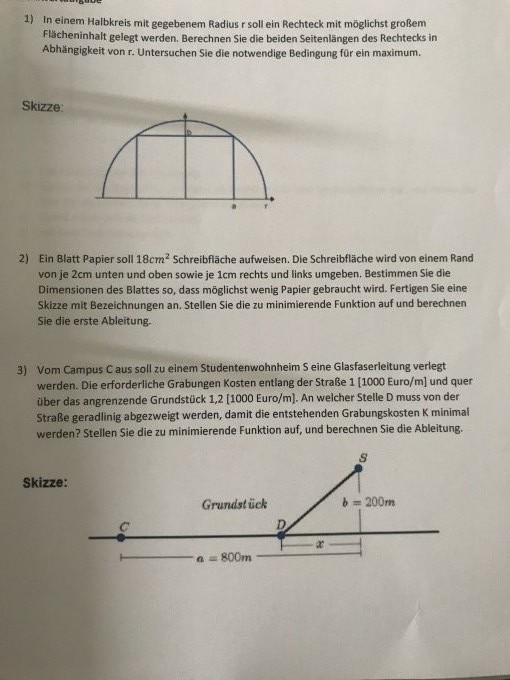
Es geht und Aufgabe 1) und 3)
Aufgabe 1) habe ich:
Hauptbedingung: A= a*b
Nebenbedingung: r = sqrt(b^2/4 + a^2)
(Nach Satz des Pythagoras)
Bin mir aber unsicher ob es richtig ist!
Und bei Aufgabe 3 komme ich überhaupt nicht weiter, wie die Haupt-bzw. Nebenfunktion ausehen könnte!
Würd mich freuen wenn mir jemand helfen könnte
mfg