Optimierungsaufgabe:
Vom Campus C aus soll zu einem Studentenwohnheim S eine Glasfaserleitung verlegt werden (siehe Skizze). Die erforderlichen Grabungen kosten entlang der Straße 1 [1000 €/m] und quer über das angrenzende Grundstück 1,2 [1000 €/m]. An welcher Stelle D muss von der Straße geradlinig abgezweigt werden, damit die entstehenden Grabungskosten K minimal werden? Stellen Sie die zu minimierende Funktion auf, und berechnen Sie die Ableitung.
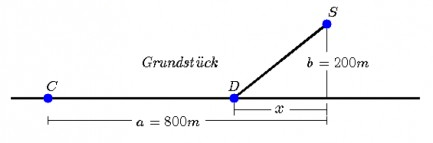
Mir fehlt hier der Ansatz, also überhaupt der Weg, die Funktionsgleichung aufzustellen.