In der euklidischen Ebene ℝ² seien folgende Punkte gegeben:
$$\left( \begin{array} { l } { - 3 } \\ { - 4 } \end{array} \right) , \quad \left( \begin{array} { c } { - 1 } \\ { - 1 } \end{array} \right) , \quad \left( \begin{array} { l } { 0 } \\ { 1 } \end{array} \right) , \quad \left( \begin{array} { l } { 2 } \\ { 3 } \end{array} \right) , \left( \begin{array} { l } { 4 } \\ { 5 } \end{array} \right)$$
1) Berechnen Sie nach der Methode der kleinsten Fehlerquadrate die Ausgleichsgrade y=α+βx zu diesen Punkten.
2) Berechnen Sie den Abstand der Ausgleichsgrade vom Ursprung.
Diese Aufgabe habe ich erst händisch, dann mit nem Spreadsheet zu lösen versucht:
demnach wäre die Geradengleichung:
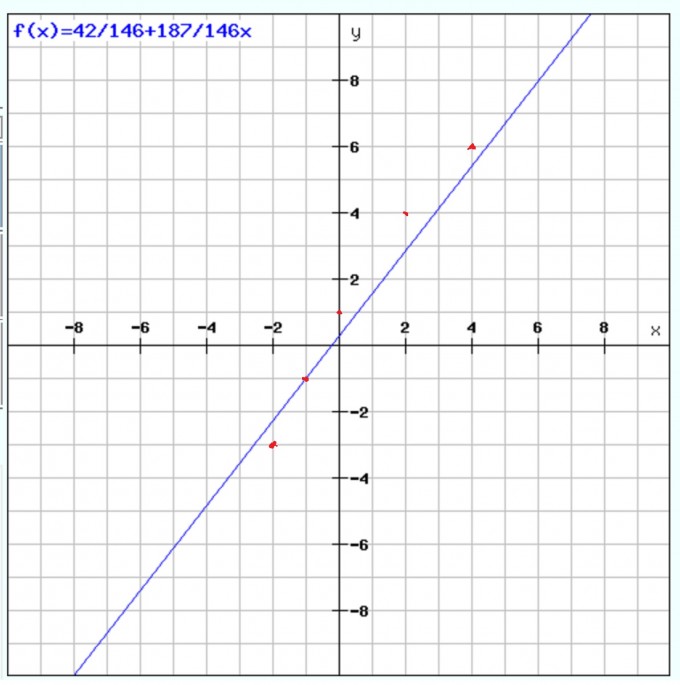
y = 42/146 + 187/146x
Da es sich um eine Klausuraufgabe handelt und wir keinen Taschenrechner benutzen dürfen, bin ich mir unsicher ob das so gewollt ist, insbesondere, da die Gerade einen nicht grad optimalen Eindruck macht:
Mein Ansatz zur Lösung war folgender:
\( μ \begin{pmatrix} -\frac{187}{146}\\1 \end{pmatrix} = \begin{pmatrix} 0\\ \frac{42}{146} \end{pmatrix} + λ·\begin{pmatrix} 1\\ \frac{187}{146} \end{pmatrix} \)
allerdings unterlaufen mir dabei Fehler, wie es scheint.
Wisst ihr eventuell wie sich diese Aufgabe eleganter lösen ließe?