ich wusste nicht, was für nen Titel ich wählen sollte.. hoffe das geht so in Ordnung.
es geht um diese Aufgabe:
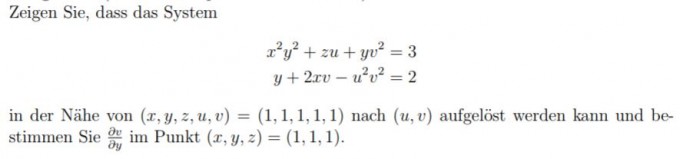
Teil 1:
Also ich habe erstal Die jacobi matrix gebildet. jeweils nach (u,v) und dann den Punkt (1,1,1,1,1) eingesetzt. Die Determinante war dann != 0 und ist soweit in Ordnung glaub ich mal...
Teil 2:
Nun habe ich die Jacobi gebildet, indem ich nach x,y,z ableite. Habe hier den Punkt wieder eingesetzt und bekam die Folgende Matrix raus. (siehe Bild ganz unten). gesucht ist nun \(\frac{dv}{dy} (1,1,1)\).
Ich weiß nicht mehr weiter. aber ich muss wahrscheinlich etwas mit der zuvor ausgerechneten Matrix machen. oder soll ich jetzt diese matrix \(\begin{pmatrix}2 & 3 & 1 \\ 2 & 1 & 0 \end{pmatrix}\) einfach nach y ableiten und (1,1,1) einsetzen?

mfg