Betragsrechnung. Unterschiede von |x| + |y| ≤ 2 und |x + y| ≤ 2 feststellen

Question

Wir sollen von der uni aus die Unterschiede zwischen |x| + |y| <= 2 und |x+y| <= 2 feststellen. Im Anhang befindet sich mein Rechenweg, jedoch bin ich mir nicht sicher ob dieser so richtig ist und vor allem verstehe ich nicht wie ich die Ergebnisse zu interpretieren habe. Über Hilfe wäre ich sehr dankbar.

MfG

Steven

Comments

Sollst du die angegebenen Punktmengen in die Koordinatenebene zeichnen?

Answer 1

Achtung: Wenn du durch (-1) teilst, dreht sich das Ungleichheitszeichen ohne, dass die Gleichheit weggeht.

D.h. aus ≤ wird ≥ und nicht > . Da hast du Fehler in deiner Rechnung.

Sollst du die angegebenen Punktmengen in die Koordinatenebene zeichnen?

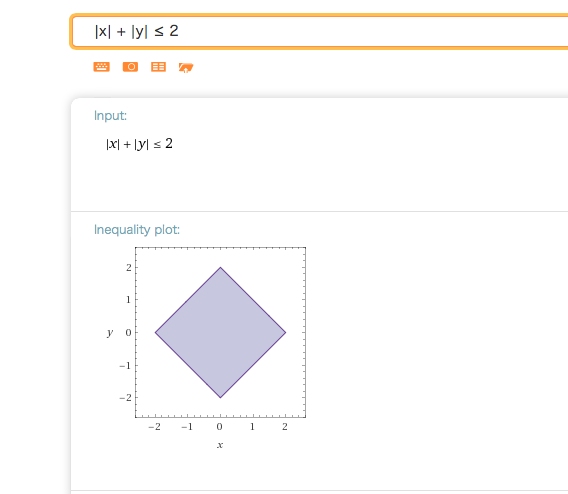
 Zu (1) eine Zeichnung:

Deine 4 Fälle enstprechen den 4 Quadranten und geben als Grenzen des gesuchten Gebiets Geradenstücke in den 4 Quadranten.

https://www.wolframalpha.com/input/?i=%7Cx%7C+%2B+%7Cy%7C+≤+2

Bei (2) ergibt sich ein (unendlich langer) Streifen im Koordinatensystem.

Du hast die beiden Begrenzungslinien ausgerechnet und herausgefunden, dass alles zwischen diesen beiden Linien (inklusive beide Linien) zur Punktmenge gehören.

https://www.wolframalpha.com/input/?i=%7Cx+%2B+y%7C+≤+2

Answer 2

Unterschiede zwischen |x| + |y| <= 2 und |x+y| <= 2

Z.B.: Für x=3 gibt es links kein y und rechts -5<y<-1.