Mit den Gleichungen sind Vektorgleichungen gemeint.
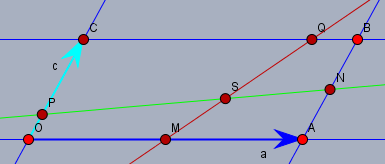
Dann ist:
$$\vec{MQ} = -\vec{OM} + \vec{OC} + \vec{CQ} = -\frac12 \vec{a} + \vec{c} + \frac{5}{6} \vec{a} = \frac13 \vec{a} + \vec{c} \\ \vec{PN} = -\vec{OP} + \vec{OA} + \vec{AN} = -\frac14 \vec{c} + \vec{a} + \frac12 \vec{c} = \frac14 \vec{c} + \vec{a} $$ damit kannst Du auf Basis dieser Vektoren zwei Geradengleichung aufstellen ...
$$\vec{s} = \frac12 \vec{a} + u \cdot \vec{MQ} \\ \vec{s} = \frac14 \vec{c} + v \cdot \vec{PN}$$
... und diese zum Schnitt bringen, d.h. gleichsetzen und für die Richtungsvektoren die obigen Ausdrücke für \(\vec{MQ}\) und \(\vec{PN}\) einsetzen:
$$\frac12 \vec{a} + u \cdot \left( \frac13 \vec{a} + \vec{c}\right) = \frac14 \vec{c} + v \cdot \left( \frac14 \vec{c} + \vec{a}\right)$$ Jetzt sortiere das so, dass nur noch Faktoren vor \(\vec{a}\) und \(\vec{c}\) übrig bleiben:
$$\left( \frac12 + \frac{u}{3} - v\right) \vec{a} - \left( \frac14 + \frac{v}{4} - u\right) \vec{c} = \vec{0} $$ Damit diese Gleichung aufgeht, müssen die Faktoren vor den Vektoren zu 0 werden. Daraus folgt ein lineares Gleichungssystem mit zwei Unbekannten:
$$2u - 6v = -3 \\ -4u + v = -1$$ und den Lösungen $$u=\frac{9}{22}; \, v=\frac{7}{11}$$ Setzt Du dies in eine der Geradengleichung für \(\vec{s}\) ein, so erhältst Du die gewünschte Lösung: $$\begin{aligned} \vec{s} &= \frac12 \vec{a} + \frac{9}{22} \cdot \left( \frac13 \vec{a} + \vec{c}\right) \\ &= \frac{7}{11} \vec{a} + \frac{9}{22} \vec{c} \end{aligned}$$