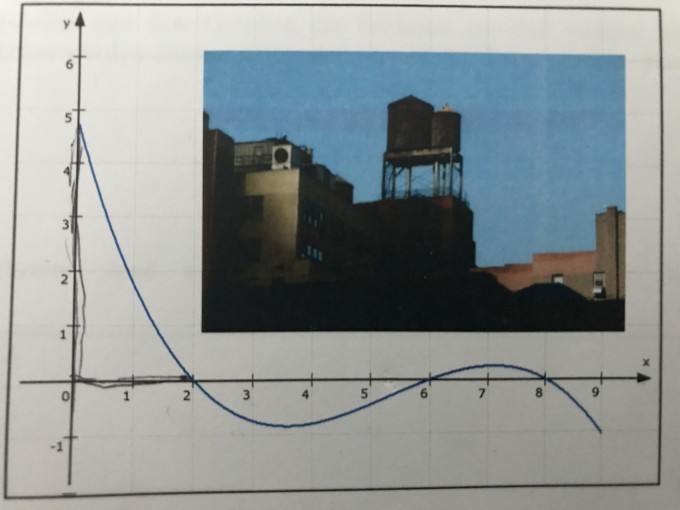
Wolkenkratzer in New York haben häufig einen Wasserspeicher auf den Dach installiert, um den Wasserbedarf im Gebäude sicherzustellen. Der anfängliche Füllstand beträgt 5 m^3.
Funktionsgleichung:
v(t) = -0,05t^3 + 0,8t^2 - 3,8t + 4,8
Das Intervall lautet [0;9]
t = std
v(t) = m^3/h
a) Ermittle den rechnerischen Nachweis, zu welchem Zeitpunkt die Entnahmegeschwindigkeit am größten ist und gib den Wert an.
b) Bestimme den Zeitpunkt, in dem die Zulaufgeschwindigkeit am stärksten zunimmt.
c) Ermittle den Zeitpunkt mit dem höchsten Füllstand und gib den Wert an.
d) Berechne den Füllstand am Ende der betrachteten Zeitspanne.
Meine Ideen:
Zu a) das ist die tiefste Stelle korrekt ?
b) das ist die stelle die nach der tiefsten Stelle kommt ?
c ) ...
d ) hier der letzte Wert der x-Achse in v(t) einsetzen ?