Mit Venn-Diagramm sieht es dann so aus:
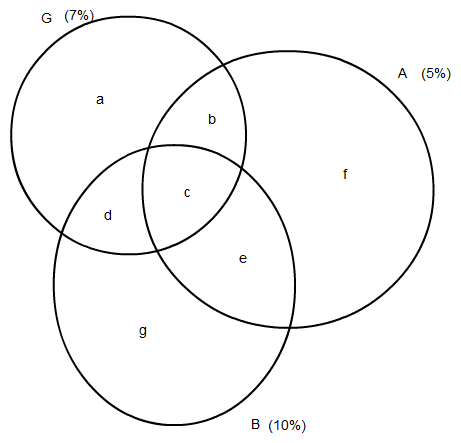
Und aus " Nur bei 40% der letztgenannten Fälle tritt kein weiterer Fehler auf;"
folgt schon mal g=4%
und aus "bei 30% stimmt auch das Aufmaß nicht "
folgt c+e=3% und aus "In 1% aller ausgelieferten Küchen stimmt nur das Aufmaß nicht."
folgt e=1% also damit auch c = 2%.
Damit man bei B auf 10% kommt, muss also d=3% sein.
Nun fehlen noch a,b und f.
Damit man auf G=7% kommt, muss gelten a+b=2%
und für A=5% muss gelten b+f = 2%
==> a+2b+f=4%
Außerdem wäre a+b+f=5%, wenn alle Fehler beanstandet
werden. Dann müsste aber b= -1% sein. Das macht wenig
Sinn, also werden wohl nicht alle beanstandet und wie bei
der Lösung vom Mathecoach lässt man das einfach weg
und hat eine Lösung mit a=b=f=1%.
Oder auch a=f=1,5% und b=0,5%.