statt des Graphen der Sinusfunktion würde ich Dir den Einheitskreis als Anschauungshilfe empfehlen.
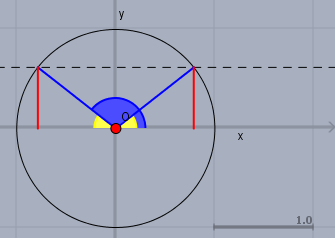
Der Sinus ist definiert als das Verhältnis von Gegenkathete (rot) zu Hypotenuse (blau) im rechtwinkligen Dreieck. Im Einheitskreis ist die Hypotenuse immer \(=1\) - also entspricht die Länge der Gegenkathete (rot) immer dem Wert des Sinus.
Im Bild sind zwei Winkel (gelb und blau) eingetragen, deren Summe \(=\pi\) ist - also der Halbkreis. Es ist offensichtlich, dass man für diese beiden Winkel immer den gleichen Wert für den Sinus erhält. Die gestrichelte Linie läuft parallel zur X-Achse, da die beiden entstehenden rechtwinkligen Dreiecke konkruent sind.