Bestimmen Sie die allgemeine Tangentengleichung an den Graphen von f im Punkt P \((u|f(u))\).
\(f(u) = - \frac{1}{4} u^2 + 4\)
\(f'(x) = - \frac{1}{2} x\)
\(f'(u) = - \frac{1}{2} u\)
Punkt-Steigungsform einer Geraden:
\(\frac{y- (- \frac{1}{4} u^2 + 4)}{x-u}=-\frac{1}{2}u\)
\(\frac{y+ \frac{1}{4} u^2 - 4}{x-u}=-\frac{1}{2}u\)
\(y+ \frac{1}{4} u^2 - 4=-\frac{1}{2}u(x-u)\)
\(y+ \frac{1}{4} u^2 - 4=-\frac{1}{2}ux+\frac{1}{2} u^2\)
\(y=-\frac{1}{2}ux+\frac{1}{4} u^2+4\)
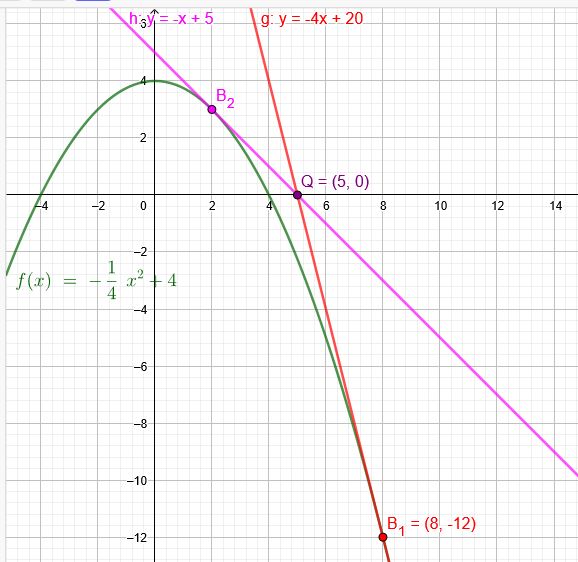
Welche Tangenten an den Graphen von f schneiden die x- Achse im Punkt Q\((5|0)\).
\(\frac{1}{4} u^2-\frac{5}{2}u+4=0\)
\( u^2-10u=-16\)
\( (u-5)^2=-16+25=9|±\sqrt{~~}\)
1.)
\( u-5=3\)
\( u_1=8\) \(f(8) = -12\)
2.)
\( u-5=-3\)
\( u_2=2\) \(f(2)=3\)
1. Tangente:
\(y=-4x+20\)
2. Tangente:
\(y=-x+5\)