Berechnung von reellen Funktionen: f1 (x)= -6x^2-5x-6,4 und f2(x)= 14/15x^2+5 11/15x +2 4/5.

Question

Hall brauch eure Hilfe,

 

Gegeben sind die reellen Funktionen f₁ (x)= -6x²-5x-6,4 und

f₂(x)= 14/15x²+5 11/15x +2 4/5.

 

a) Bestimmen Sie die Schnittpunkte S1 und S2 der Graphen der beider Funktionen.

 

b) Ermitteln Sie de Funtionsterm der Funtion, deren Graphen S1 und S2 verbindet.

 

c) Ermitteln Sie die Achsenschnittpunkte aller drei Funktionen.

 

d) Zeichen Sie die Graphen aller drei Funktionen

 

danke schon mal.

Answer 1

f1(x) = - 6·x^2 - 5·x - 6.4 = - 6·x^2 - 5·x - 32/5

f2(x) = 14/15·x^2 + (5 + 11/15)·x + (2 + 4/5) = 14/15·x^2 + 86/15·x + 14/5

a) Bestimmen Sie die Schnittpunkte S1 und S2 der Graphen der beider Funktionen.

f1(x) = f2(x)

- 6·x^2 - 5·x - 32/5 = 14/15·x^2 + 86/15·x + 14/5

- 90·x^2 - 75·x - 96 = 14·x^2 + 86·x + 42

- 104·x^2 - 161·x - 138 = 0

104·x^2 + 161·x + 138 = 0

Keine Schnittpunkte da die Diskriminante negativ ist.

Daher hier jetzt eine Nachfrage. Habe ich die Funktionsterme richtig gedeutet? Wenn ja würde es keine Schnittpunkte geben. Und dann kann man b) auch nicht machen. 

Also schau mal bitte nach der Richtigkeit der Funktionen.

Comments

Ja die Funtktionen stimmen.Dann wird das wohl nicht gehen trotzdem danke.

---

Nein sry hab den fehler gefunden Funktion lautet f₁(x)= -0,6x²-5x-6,4

---

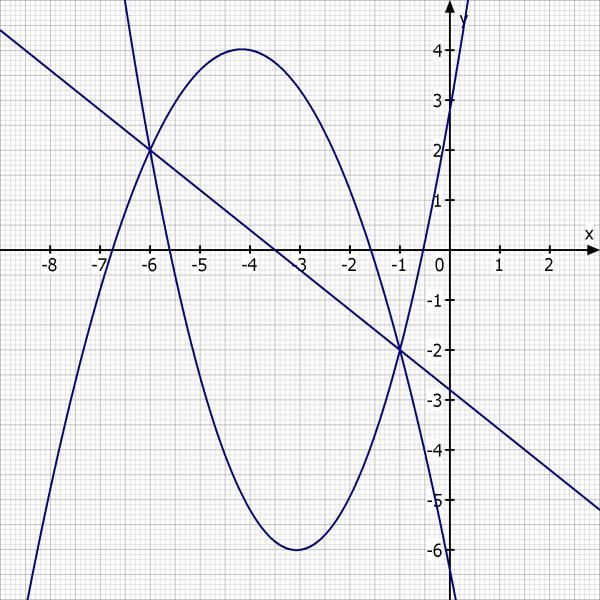
f1(x) = - 0.6·x^2 - 5·x - 6.4 = - 3·x^2/5 - 5·x - 32/5

f2(x) = 14/15·x^2 + (5 + 11/15)·x + (2 + 4/5) = 14/15·x^2 + 86/15·x + 14/5

a) Bestimmen Sie die Schnittpunkte S1 und S2 der Graphen der beider Funktionen.

f1(x) = f2(x)

- 3·x^2/5 - 5·x - 32/5 = 14/15·x^2 + 86/15·x + 14/5

x = -6 ∨ x = -1

f1(-1) = -2

f1(-6) = 2

b) Ermitteln Sie de Funtionsterm der Funtion, deren Graphen S1 und S2 verbindet.

Es sollen die Punkte [-1, -2] und [-6, 2] verbunden werden

f(x) = (2 - (-2)) / (-6 - (-1)) * (x - (-1)) - 2 = - 4/5·x - 14/5

c) Achsenschnittpunkte solltest du selber finden

d) Ich übernehme mal die Skizze, damit du die Achsenschnittpunkte erkennen kannst.