Hallo IE,
(x + 2)2 - 1 = 0.5·(x + 2)2 + 3.5 | - 0.5·(x + 2)2
0.5 * (x + 2)2 - 1 = 3.5 | +1 | : 0.5
(x + 2)2 = 9 | √
x + 2 = ± 3
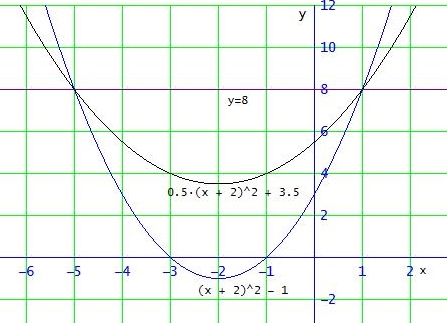
x1 = 1 → y1 = 8 , P1 (1 | 8 )
x2 = - 5 → y2 = 8 , P2 (-5 | 8 )
Die gesuchte Gerade ist y = 8 (Parallele zur x-Achse)
Gruß Wolfgang