Untersuchen Sie die beiden auf ℝ definierten reellen Funktionen
f1 und f2, gegeben durch
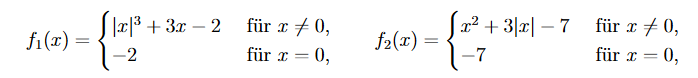
Text erkannt:
\( f_{1}(x)=\left\{\begin{array}{ll}|x|^{3}+3 x-2 & \text { für } x \neq 0, \\ -2 & \text { für } x=0,\end{array} \quad f_{2}(x)=\left\{\begin{array}{ll}x^{2}+3|x|-7 & \text { für } x \neq 0, \\ -7 & \text { für } x=0,\end{array}\right.\right. \)
an der Stelle x0 = 0 auf Stetigkeit, linksseitige Differenzierbarkeit, rechtsseitige Diffe-
renzierbarkeit sowie Differenzierbarkeit. Im Fall der Differenzierbarkeit bestimmen Sie
für x0 = 0 den Wert der Ableitung und die Gleichung der Tangente.