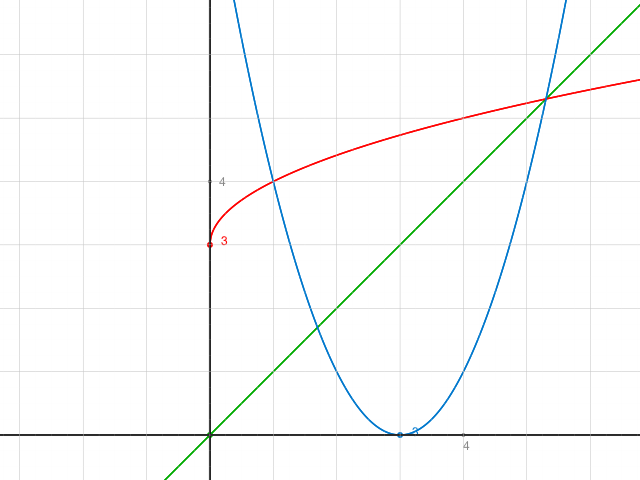
a)
x2+2x = y
oder
x^2 + 2x - y = 0 ist lösbar genau dann, wenn die Diskriminante d dieser quadr. Gleichung d = b^2 -4ac ≥ 0
d = 4 + 4y ≥ 0
1+y ≥ 0
y ≥ -1
eindeutig lösbar ist a) falls d = 0. d.h. y = -1
h ist injektiv
und
g ist nicht injektiv. Begründung: g(-0.5) = g(0.5).
Hier noch der Graph von h:
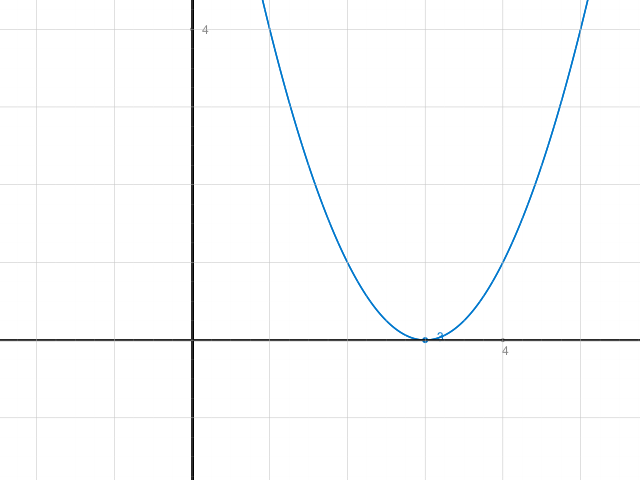
ab x = 3 ist er streng monoton steigend. Daher ist die Funktion bijektiv.
y = (x-3)^2 auflösen nach x
±√y = x-3
3 ± √y = x
Umkehrfunktion hat die Gleichung y = 3 + √x
Da blau erst für x ≥ 3 gilt, muss bei der Spiegelung an y=x das + stehen und nicht das -