Aufgabe 3:
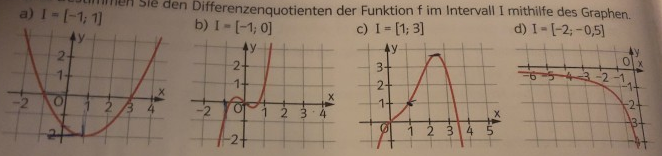
Bestimmen Sie den Differenzenquotienten der Funktion f im Intervall I mit Hilfe des Graphen.
a) I = [-1; 1]
b) I = [-1; 0]
c) I = [1; 3]
d) I = [-2; 0.5]
Aufgabe 4:
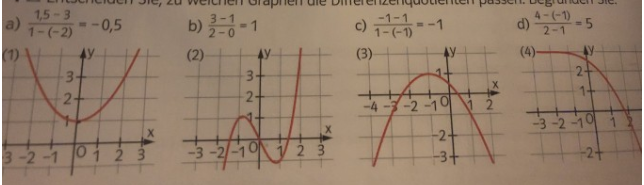
Entscheiden Sie, zu welchen Graphen die Differenzenquotienten passen. Begründen Sie.
a) \( \frac{1,5-3}{1-(-2)}=-0,5 \)
b) \( \frac{3-1}{2-0}=1 \)
c) \( \frac{-1-1}{1-(-1)}=-1 \)
d) \( \frac{4-(-1)}{2-1}=5 \)