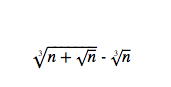Grenzwert von Differenz von Wurzeln bestimmen

Question

Aufgabe:

Beweisen, dass der Grenzwert der folgenden Folge 0 sein muss.

$$\lim\limits_{n\to\infty}$$

\( \sqrt[3]{n+\sqrt{n}} \) - \( \sqrt[3]{n} \)

Problem/Ansatz:

Ich würde gerne wissen wie ich beweisen kann, dass der Grenzwert für die obige Gleichung 0 sein muss.

Der Grenzwert von beiden Wurzeln separat betrachtet ist ja unendlich. Ist der Grenzwert 0, da unendlich minus unendlich (nur in der Grenzwertbetrachtung) 0 ergibt??

Wie sähe dann der richtige Beweis aus?

MfG

Comments

Das ist keine Gleichung. Und wohin soll n gehen?

---

n soll wohl gegen unendlich gehen.

---

Term, keine Gleichung.

Ja, \( \lim\limits_{n\to\infty} \)

Answer 1

   | unten die Drittel für dritte Wurzeln

=( ( ^3√(n+√n) )^3 - ( ^3√(n))^3) / ((n+√n)^(2/3) + ((n+√(n))n)^(1/3) + n^(2/3))

= ( (n+√n)  - n) / ((n+√n)^(2/3) + ((n+√(n))n)^(1/3) + n^(2/3))

= ( n^(1/2) / ((n+√n)^(2/3) + ((n+√(n))n)^(1/3) + n^(2/3))     | das ist sicher grösser als 0

                                         mache den Nenner etwas kleiner. ==> Bruchwert grösser

<   n^(1/2) / ((n)^(2/3) + (n*n)^(1/3) + n^(2/3))

=  n^(1/2) / (3*(n)^(2/3) )

= 1/3^(2/3) * 1/n^(2/3 - 1/2)

= 1/3^(2/3) * 1/n^(1/6)        hat den Grenzwert 0.

Es folgt: Der Grenzwert von

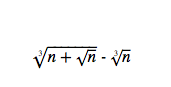  ist ≥ 0 und gleichzeitig ≤ 0. D.h. er ist Null.

(Sandwich-Lemma)

Comments

Vielen Dank! Ich habe es nun verstanden nachdem Ich es auf ein Blatt aufgeschrieben habe. 

---

Bitte. Gern geschehen!

Answer 2

sei

a=n-sqrt(n) und b=sqrt(n)

Erweitere dem Term nun mit

(a^(2/3)+(ab)^(1/3)+b^(2/3))

ähnlich der dritten binomischen Formel.

Dann bleibt im Zähler n^(1/2) stehen und im Nenner erhälts du Terme der Ordnung n^(2/3). Also ist der Nennergrad höher als der Zählergrad, die Folge strebt also gegen 0.

Comments

danke für die Antwort!

Von wo kommt das a = n - \( \sqrt{n} \) und b = \( \sqrt{n} \) her?

Kann ich einfach a = \( \sqrt[3]{n+\sqrt{n}} \)

und b = -\( \sqrt{n} \) setzen

Und dann erweitern?

Nein, diesen Schritt verstehe Ich leider nicht.... =(

Ich habe versucht, die Wurzel zu radizieren. Dann müsste doch \( \sqrt[3]{n} \) +  \( \sqrt[6]{n} \) - \( \sqrt[3]{n} \) rauskommen, was aber ein Widerspruch zum Grenzwert = 0 ist....

:(

---

Von wo kommt das a = n - n−−√ und b = n−−√ her?

Das ist eine Festlegung, um Schreibarbeit zu sparen. Hat eigentlich gar keinen inhaltlichen Wert.

Kann ich einfach a = n+n−−√−−−−−−√3

und b = -n−−√ setzen

Und dann erweitern?

Ja, aber dann hast du eine sinnfreie Umbenennung gewählt und verliert Informationen über den Term. a-b kann man nicht sinnvoll erweitern.

Ich habe versucht, die Wurzel zu radizieren. Dann müsste doch n−−√3 +  n−−√6 - n−−√3 rauskommen, was aber ein Widerspruch zum Grenzwert = 0 ist....

Das ist auch falsch gemacht. Das entspricht nicht den Wurzelgesetzen.

Du darfst nicht einfach aus jedem Summanden die Wurzel ziehen.

---

Ich verstehe es leider immer noch nicht. Wie würde der Lösungsweg denn in der richtigen Variante aussehen? Dann sollte Ich es nachvollziehen können.

MfG

Answer 3

es gilt

a³-b³=(a-b)(a²+ab+b²)

Umgekehrt ist also

$$a-b=\frac{a³-b³}{a²+ab+b²}$$

In deiner Aufgabe besteht (a-b) aus der Differenz der beiden gegebenen dritten Wurzeln.

Wende das nun an.

Comments

Ich verstehe es immer noch nicht. Welche Werte soll ich nun für a und welche Werte für b verwenden?

Ich versuche jetzt diese Aufgabe seit 2 Tagen zu lösen. Ich würde mich über einen Lösungsweg freuen - sodass es im Hirn "tick" macht.

MfG

---

Das ist ein Trick so ähnlich wie der 3. Binom, wenn es um eine Differenz von zwei zweiten Wurzeln geht.

D.h. du merkst dir diesen Trick am besten gleich.

Erweiterung mit der "verallgemeinerten 3. binomischen Formel". 

Als Repetition: Bei Quadratwurzeln sieht die Rechnung so aus: https://www.mathelounge.de/116959/grenzwert-lim-n-n-3n-n-2n-differenz-von-wurzeln

---

Ich verstehe den Vorgang (einigermaßen) für \( \sqrt{x} \) allerdings bereitet mir hier \( \sqrt[3]{x} \) Kopfschmerzen. Als ob das nicht reicht, habe Ich auch noch eine Wurzel zweiten Grades in der Wurzel dritten Grades.....

Ok, Ich habe erst einen Bruch hierraus gemacht dann dies oben und unten erweitert. Allerdings macht es überhaupt keinen sinn, Ich habe nun oben den selben Term stehen und unten auch fast den selben nur nun dass es statt der 3-ten Wurzel die 2/3-te Wurzel ist.

---

Am besten machst du mal ein gut lesbares Foto von deiner Rechnung.

Gast 2144 hat doch beschrieben, wie dein Bruch nach dem Einsetzen aussehen sollte.

Ein Quadratwurzel im Zähler ist kein grosses Hindernis. Damit kann man weiterrechnen. Hauptsache ist, dass das Minus bei "unendlich minus unendlich" weg ist, da du da unmöglich abschätzen kannst, was herauskommt.

---

Gerne! Hier, bitte:

Bild wird auf Windows normal angezeigt aber hier gedreht..... ?

---

Im Zähler sollte

√n + n - n = √n stehen.

Du hattest in der Zeile darüber noch ein minus im Zähler.

---

Danke. :D Da blitzt es mir im Hirn.... reicht es hier schon sagen, dass der Nenner größer als der Zähler ist, und dass somit die Reihe Konvergiert und gegen 0 strebt?

Denn \( \frac{\sqrt n}{∞} \) = 0 (nicht wirklich der Fall, aber vom Gedanken her passt es)

---

Du musst den Grad des Zählers und des Nenners anschauen.

D.h. eigentlich oben und unten durch n^(1/2) dividieren.

Dann bleibt unten im Prinzip n^(1/6) und oben hast du 1.

In diesem Moment ist der Grenzwert dann klar Null.