Veranschaulichen Sie diesen Zusammenhang der Produktregel im Zusammenhang mit einem Beispiel

Question

Der Graph der Funktion f berührt die x-Achse im Punkt P (2/0)

Zeigen Sie, dass der Graph von g mit g(x)=x*f ebenfalls die x-Achse im Punkt P berührt.

Wie rechnet man das aus?

Answer 1

Hallo

 du weisst f(2)=0 und f'(2)=0 jetzt berechne g(2) und g'(2) nach der Kettenregel.

Gruß lul

Comments

woher weiss ich das?

---

Hallo

 f(x) geht durch (2,0) deshalb f(2)=0 f berührt da die x- Achse also ist x Achse waagrechte Tangente also f'(2)=0

grüß lul

---

ok das habe ich nun verstanden also rechne ich nun g(2)= 2*f(2)= ?

---

Hallo lul,

... berechne g(2) und g'(2) nach der Kettenregel

      du meinst wohl eher f(2), f '(2) und die Produktregel

Gruß Wolfgang

---

Sorry,  bei "du meinst wohl eher f(2), f '(2)" habe ich mich vertan (musste meine ganze Aufgabe ändern.

Aber die Produktregel bleibt :-)

Answer 2

Hallo Anna,

Der Graph der Funktion f berührt die x-Achse im Punkt P (2/0)

Der Graph einer Funktion "berührt" die x-Achse in (2|0)  genau dann, wenn er dort einen Tief- oder einen Hochpunkt hat

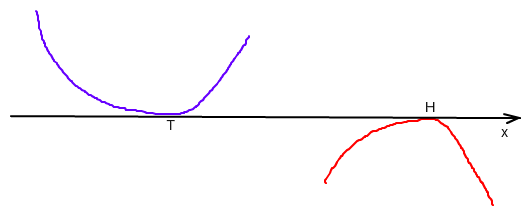
Deshalb gilt  f(2) = 0  und  f'(2) = 0

 g(x) = x · f(x)   hat nach der Produktreglel  [u·v] ' = u' · v + u · v'  die Ableitung

g'(x)  = 1 · f(x)  +  x · f'(x)  =  f(x) + x · f'(x)

Deshalb gilt g(2) = 2 · f(2)  = 2 · 0  = 0  

           und  g'(2)  =  f(2) + 2 · f'(2)  =  0 + 2 · 0  = 0 

g berührt also in P(2|0) die x-Achse.

----------

Nachtrag:

Veranschaulichen Sie diesen Zusammenhang an einem Beispiel:

f(x) = (x-2)²   ,   g(x) = x·(x-2)² 

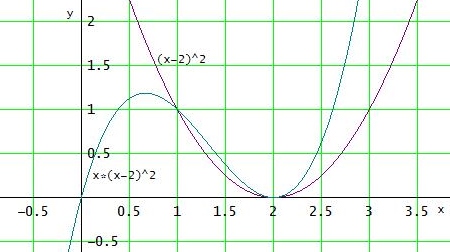
Gruß Wolfgang