Extrempunkte bestimmen (gebrochen rationale Funktionen) f(x) = (x^3 - 16x)/(1-x^2)

Question

Woher weiß ich, dass diese Funktion keine Extrempunkte hat?

Aufgabe:

$$f ( x ) = \frac { x ^ { 3 } - 16 x } { 1 - x ^ { 2 } }$$

Ansatz:

Mit der Quotientenregel:

(51x²-5x⁴-16)/((1-x²)²)

Ich habe dann mit dem Zähler eine Gleichung aufgestellt

(51x²-5x⁴-16) = 0

Das kann man mit der Substituion lösen x^2=u

51u-5u²-16=0

Laut meinen Lösungen gibt es jedoch keine Extrempunkte, warum nicht?

f(x) = (x^3 - 16x)/(1-x^2) 

Answer 1

f(x) = (x^3 - 16x)/(1-x^2)

Kontrolliere deine Ableitung.

Es kann vorkommen, dass quadratische Gleichungen keine Lösungen haben.

Es gibt gelegentlich auch Terrassenpunkte.

Ausserdem den blauen Teil nicht ignorieren:

Ein Bruch ist genau dann 0, wenn der Zähler 0 und der Nenner nicht 0 ist. 

Kontrolliere, ob bei deinen "Lösungen der Nenner 0 ist". 

Schau mal, was wolframalpha zu deiner Funktion meint. https://www.wolframalpha.com/input/?i=(x%5E3+-+16x)%2F(1-x%5E2)

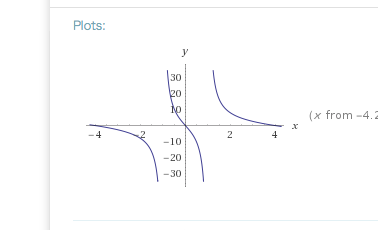
Gut möglich, dass hier die Ableitung nie exakt 0 ist. 

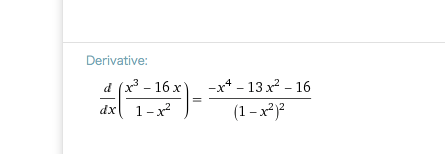
(51x^{2}-5x^{4}-16) = 0

Hast du hier einen Vorzeichenfehler in deiner Rechnung?

Answer 2

die 1. Ableitung lautet:

y '= (-x^4 - 13 x^2 - 16)/(1 - x^2)^2

y'=0 =(-x^4 - 13 x^2 - 16)

--->keine reellen Lösungen, nur komplexe Lösungen

->keine Extrempunkte

Answer 3

Schreibe den Funktionsterm so: (x(x+4)(x-4))/((1-x)(1+x)).

Dann sieht man: Der Graph hat (von links nach rechts) eine Nullstelle mit Vorzeichenwechsel, dann einen Pol ohne Vorzeichenwechsel, dann wieder eine Nullstelle mit Vorzeichenwechsel, dann einen Pol ohne Vorzeichenwechsel und noch eine Nullstelle mit Vorzeichenwechsel. Außerdem ist g(x)=-x Asymptote. Wenn du das alles berücksichtigst, ergibt sich dieses Bild: