Aufgabe:
Eine Volkswirtschaft bestehe aus den drei Sektoren Ackerbau, Industrie und Viehzucht. Der Ackerbau produziert Weizen, die Viehzucht produziert Schweine und die Industrie produziert Eisen. Die drei Sektoren beliefern einander und halten dadurch die Produktion aufrecht. Außerdem beliefern sie den Endverbrauch.
Im Einzelnen gilt:
Der Ackerbau produziert 1040q Weizen und benötigt dafür 80q Weizen, 40t Eisen und 190 Schweine.
Die Industrie produziert 720t Eisen und benötigt dafür 60q Weizen, 110t Eisen und 140 Schweine.
Die Viehzucht produziert 1150 Schweine und benötigt dafür 200q Weizen, 70t Eisen und 120 Schweine.
Die restlichen Güter sind für den Endverbrauch bestimmt.
Es sollen die Lieferungen der Viehzucht an den Endverbrauch verdoppelt werden.
Wie viel Eisen wird nach der Anpassung produziert?
Hinweise: Rechnen Sie mit 4 Nachkommastellen und runden Sie die gesuchten Ergebnisse erst am Ende auf 2 Nachkommastellen. Außerdem benötigen Sie eine der beiden folgenden inversen Matrizen:
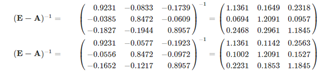
Problem/Ansatz:
Wie berechne ich wie viel Eisen produziert werden müssen und woher weiß ich welche der oben genannten Matrizen ich verwenden muss?