Streckenverhältnis (gleichseitige Dreiecke)

Question

 Das Dreieck ABC sei gleichseitig. L, H und M seien die Seitenmitten. Die Dreiecke EMD und FLE seien kongruent zu ABC. Bestimme das Längenverhältnis der Strecken EH und CH.

Comments

 

EH / CH  =  LN / LM

---

Sehr schöne Ergänzung.

---

Das scheint eine Drehstreckung um den Schnittpunkt von HC und LM mit dem Streckungsfaktor 1/√3 zu sein.

Ich sehe nur nicht den geometrischen Hintergrund und bin auf die Auflösung gespannt.

---

bin auf die Auflösung gespannt

Es ist einfach eine andere Art, Φ mittels eines gleicheitigen Dreiecks zu konstruieren und wurde 1983 als Problem Nr. E3007 im American Mathematical Monthly veröffentlicht.

Answer 1

Hallo Roland,

das Verhältnis lässt sich mit einem simplen Pythagoras bestimmen. Man beachte das Dreieck \(\triangle ZME\):

Die Strecke \(LM\) ist die Mittelparallele  - d.h. \(|CZ| = \frac 12 |CH|\) - und nach Pythagoras gilt $$\begin{aligned}|EZ| &= \sqrt{|EM|^2 - |ZM|^2} \\ |EZ| &= |EM| \sqrt{1- \left( \frac14 \right)^2} = \frac 14 \sqrt{15} \, |EM| \end{aligned}$$ Daraus folgt dann: $$\begin{aligned}  \frac{|EH|}{|CH|} &= \frac{|EZ| + \frac14 \sqrt 3\, |EM|}{\frac12 \sqrt 3 \,|EM|} \\ &= \frac{\frac 14 (\sqrt{15} + \sqrt 3)}{\frac12 \sqrt 3 } \\ &= \frac 12 (\sqrt 5 + 1) \\ \frac{|EH|}{|CH|} &= \Phi \end{aligned}$$ Das Verhältnis entspricht also dem goldenen Schnitt.

Gruß Werner

Comments

Spitzenmäßig.

Answer 2

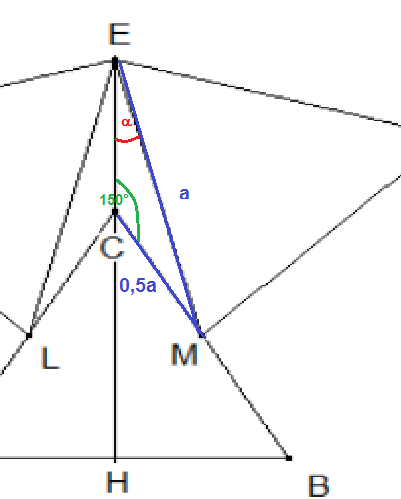
Im Dreieck CME gilt nach Sinussatz sin(α)/(0,5a)=sin150°/a.

Daraus folgt sin(α) =0,25. Über den trigonometrischen Pythagoras erhält man cos(α)=0,25√15.

Der hier nicht farbig markierte dritte Innenwinkel im Dreieck CME hat die Größe 30°-a, und unter erneuter Verwendung des Sinussatzes erhält man

CE=a*sin(30°-α)/sin(150°)

Nach Additionstheorem wird daraus

CE=a*(sin(30°)cos(α)-cos(30°)sin(α) ) /sin(150°)

CE=a*(sin(30°)*0,25√15-cos(30°)*0,25 ) /sin(150°)

Die weitere Vereinfachung dieses Terms für CE überlasse ich dem geneigten Leser.

Mit CH=0,5√3 *a lässt sich EH aus der Addition  CH + CE erzeugen dann das Verhältnis EH:CH bilden.

Comments

Das geht auch ganz ohne Winkelfunktionen und -sätze.